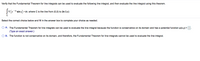
Verify that the Fundamental Theorem for line integrals can be used to evaluate the following line integral, and then evaluate the line integral using this theorem. -* sin y) • dr, where C is the line from (0,0) to (In 3,Tt) Select the correct choice below and fill in the answer box to complete your choice as needed. O A. The Fundamental Theorem for line integrals can be used to evaluate the line integral because the function is conservative on its domain and has a potential function o(x,y) = (Type an exact answer.) O B. The function is not conservative on its domain, and therefore, the Fundamental Theorem for line integrals cannot be used to evaluate the line integral.

a) Rewrite A = √=x² + 4x + 21 in the form A V 6² - (x − a)². b) Use a trigonometric substitution to evaluate the indefinite integral. S/ dx You must show all steps.

Direction: Using Riemann's Sum, find the integral of the following functions: 1.) √²(2x² - 5x + 1) dx 2.) √(x³- 2x + 1) dx 3.) f 2x³ dx

Please write out all steps taken clearly.

dx x² +9 2. Use an appropriate trigonometric substitution to rewrite J as J(a simplified trig function of 0) d0. Carefully show your work with differentials and use of trig identities to help simplify. Then find the integral. Show any use of substitutions and reasoning with right triangles.

Evaluate the definite integral

Use the second part of the Fundamental Theorem of Calculus to evaluate the following and include a sketch.

Answer all questions and explain all your steps!

I need some help on my homework

use substitution