Structural Analysis
6th Edition
ISBN: 9781337630931
Author: KASSIMALI, Aslam.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Related questions
Concept explainers
Question
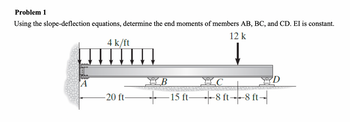
Transcribed Image Text:Problem 1
Using the slope-deflection equations, determine the end moments of members AB, BC, and CD. EI is constant.
12 k
4 k/ft
m
A
-20 ft-
B
BC
+ ·15 ft—8 ft→8 ft-
D
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 5 steps
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, civil-engineering and related others by exploring similar questions and additional content below.Similar questions
- A simple beam AB supports five equally spaced loads P (see figure). (Solve the problem by the method of superposition. The beam has constant flexural rigidity EI.) P p p B L L L L L 6 6 6 6 6 6 (a) Determine the deflection &, at the midpoint of the beam. (Enter the magnitude. Use the following as necessary: P, L, E, and I.) 8₁ = (b) If the same total load (5P) is distributed as a uniform load on the beam, what is the deflection 2 at the midpoint? (Enter the magnitude. Use the following as necessary: P, L, E, and I.) 8₂ = (c) Calculate the ratio of ₁ to 82.arrow_forward2. Determine the equations of the elastic curve for the beam using the x coordinate. (Please use thesecond-order or fourth-order integration method)(a) Specify the slope at A and maximum deflection. EI is constant.(b) Determine the deflection at the center of the beam and the slope at B. EI is constant.arrow_forwardDetermine the slope and the deflection of end B of the cantilever beam using Area-Moment Method. EI is constant.arrow_forward
- For the beam and loading shown, EI is constant. Note that the beam is statically indeterminate to the first degree. (a) Determine the equations of the elastic curve for the beam using the x coordinate. (b) Determine the slope at A. A L- wo Barrow_forward(1) Determine the equations of the elastic curve for the beam using the x and x2 coordinates. Then, find the deflection under the load P. EI is constant. Larrow_forwardUsing the virtual work method determine slope of the beam at "A". Beam is subjected to a uniformly Distributed Load “W" and a concentrated moment "WL^2" at “A" (Express the results in terms of W, L, and EI) w ikIft=constant)arrow_forward
- Determine the horizontal and vertical deflections at D for the frame shown below (consider E, I constant and neglect axial deformation). P |2L A В C 4Larrow_forwardConsider the truss shown in (Figure 1). Assume the members are pin connected at their end points. TakeA = 130 mm2, and E= 200 GPa for each member. Use the method of virtual work to solve this problem. Determine the horizontal displacement of joint D measured leftward. 8 kN 3 m 3 m 4 m C Barrow_forwardSolve the problem by the moment-area method. The beam has constant flexural rigidity EI. A simple beam AB supports two concentrated loads P at the positions shown in the figure. B C 4. 4 A support C at the midpoint of the beam is positioned at distance d below the beam before the loads are applied. Assuming that d = 12 mm, L = 5.4 m, E = 200 GPa, and I = 193 x 10° mm, calculate the magnitude of the loads P (in kN) so that the beam just touches the support at C. 163.87 x kNarrow_forward
- Determine the deflection at point D by using conjugate beam method A is a pinned and C is a roller support. E,I =constantarrow_forwardFor the beam shown, obtain: A). Applying the double integration method, the rotation in the left support (A), and the deflection in (C). B). Applying the moment of area method, the rotation in (D), and the maximum deflection between supports A and B. C). Applying the conjugate beam method, the rotation in (B), and the deflection in (D). Use the following Values: a = 1.75 m, q = 2.25 kN/m. E = 200 Gpa, |= 200 x10^6 mm^4 Note: Please provide the deflection results in mm and rotation in degrees. 90² qa A B D C аarrow_forwardProblem 2 The bar is supported by a roller constraint at B, which allows vertical displacement but resists axial load and moment. If the bar is subjected to the loading shown, determine the slope at A and the deflections at C and B. EI is constant. Use the method of direct integration. A L 3 P 1/2 C 2L 3 Barrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning
Structural Analysis (10th Edition)
Civil Engineering
ISBN:9780134610672
Author:Russell C. Hibbeler
Publisher:PEARSON
Principles of Foundation Engineering (MindTap Cou...
Civil Engineering
ISBN:9781337705028
Author:Braja M. Das, Nagaratnam Sivakugan
Publisher:Cengage Learning
Fundamentals of Structural Analysis
Civil Engineering
ISBN:9780073398006
Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel Lanning
Publisher:McGraw-Hill Education
Traffic and Highway Engineering
Civil Engineering
ISBN:9781305156241
Author:Garber, Nicholas J.
Publisher:Cengage Learning