Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
Bartleby Related Questions Icon

Related questions

Q: 26. Let A and B be (2x2) matrices. Prove or find a coun- terexample for this statement: (A - B)(A +…
A:
Q: calculate the matrix cofactor using sign convetion  + - + - - + - + + - + - - + - +
A:
Q: 5) Give an example of matrices D and F where DF is defined, but FD is not, and clearly explain why…
A:
Q: Write B as a linear combination of the other matrices, if possible. (If not, enter DNE in all…
A: This problem is related to the vector algebra. The problem is solved in the following image.
Q: Define Positive Definite Matrices.
A:
Q: ✓ 1.6 Each pair of matrices differ by one row operation. Use this operation to compare det(A) with…
A:
Q: to B=101 t00 select all true •If AB =Ithen BA=I AB=I 'AB=I but nut BA=I "BA-I inone of these %3D
A:
Q: Illustrate the multiplying any row (or column) by a scalar do to the determinant?
A:
Q: Use the matrix P to determine if the matrices A and A' are similar. -1 -1 - 13 6 6 6 P=[¯1 ¯2]·…
A:
Q: Describe all matrices which satisfy det(-A) = -det(A).
A: Assume a square matrix A of order n
Q: Use the definition of A to write the vector equation as an augmented matrix. 0 x₁ + x2 + x3 + X4 =
A:
Q: Compute A³, A-3, and A² - 2A + I. 4 0 [69 2 NOTE: Write the elements of each matrix exactly. A =
A: NOTE: Refresh your page if you can't see any equations. . the given matrix is
Q: 10 Let A = -2 1 B (Enter a matrix like -3 -6 -87 Find the product of any two of the matrices. The…
A: The rule of order (or dimension) of matrices for matrix multiplication is as follows:For two…
Q: Find the matrices of the two similarities taking (0, 0, 1) to (-2, 4, 1) and taking (1, 0, 1) to (0,…
A:
Q: 4. Explain what is wrong with the following "proof" that (ABC)" – C"B" A" for three conformable…
A: Properties of transpose of a matrix: (AB)⊥ = B⊥A⊥ Given: (ABC)⊥.
Q: True or False - Determinants of two similar matrices are the same.  Explain.
A: According to the given information, it is required to say whether the given statement is true or…
Q: what is a complex matrix? Create one hermitian complex matrix ( 3 x 3)
A: The definition of a Complex matrix and a Hermitian matrix which is a type of complex matrix is…
Q: 3) Let A and B be two matrices that are row equivalent. Show that if A is invertible, then B is also…
A: According to Bartleby guidelines , we can answer only first question. Kindly re-post other remaining…
Q: Given the points (-10,5) and (1,4) find the slope
A: Given: The points are -10,5 and 1,4. To find: The slope by using the given points.
Q: Find the inverse of the matrix 1 2 3 A-1) if A =| 2 3 1 3 1 2
A: Given,                  A=123231312
Question

Using the details of the matrices in the image, (note that they are real, and that I2 = J2 = K2 = -1 and IJ = K, show that qq* = 1. (the * term means complex conjugate)

q = (indentity matrix)q1 +q2 I + q3 J +q4 K

and

q*= (indentity matrix)q1 - q2 I - q3 J - q4 K

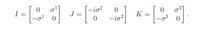
-io? I = 1 K -io? ㅇ
expand button
Transcribed Image Text:-io? I = 1 K -io? ㅇ
Expert Solution
Check Mark
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
See solutionCheck out a sample Q&A here
Step 1
VIEW
Step 2
VIEW
bartleby

Step by stepSolved in 2 steps

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Advanced Math
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Text book image
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Text book image
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Basic Technical Mathematics
Advanced Math
ISBN:9780134437705
Author:Washington
Publisher:PEARSON
Text book image
Topology
Advanced Math
ISBN:9780134689517
Author:Munkres, James R.
Publisher:Pearson,
SEE MORE TEXTBOOKS