Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
thumb_up100%
![Compica FOOLS
If the roots to the characteristic equation (3.2) are complex,' then, since the coef-
ficients of the characteristic polynomial are real, the roots are complex conjugates.
They have the form λ = a + ib and =a-ib. The corresponding solutions are
z(t) = e(+) and Z(t)=ea-ib. Using Euler's formula, these solutions become
z(t) = (a+b) =
Z(t)=ea-ib
et [cos(br) + i sin(br)]. and
=e" [cos(bt) - i sin(br)].
where
Since (t) = e-22(1), the solutions are not constant multiples of each other, so
they are linearly independent. Hence using Theorem 1.23, we see that the general
solution is
y(t) = C₁z(t) + C₂Z(r).
(3.8)
The solutions and are complex valued. Such solutions are often preferred (for
2
example, in circuit analysis). However, we are aiming for real valued solutions.
Notice from (3.7) that z and Z are complex conjugates. Written in terms of their
real and imaginary parts, we have
2(t)= y(t) +¡y₂(r) and (r) = y(t)-iys(t).
Thus we have
(3.7)
y(t) = Rez(t) = e cos(br) and y(t) = Imz(t) = esin(bt). (3.10)
+3 Linear, Homogeneous Equations with Constant Coefficienta
using complex (or real) exponentials:
sin z, cos 2, tan r, sinh r, cosh 2, tanh r
(3.9)
3) == (20)+2()) and 32(0)= (200)-2010).
Therefore, by Proposition 1.18. y() and y₂(1), the real and imaginary parts of
z(t), are solutions. Furthermore, these are real valued solutions. Since y(t) =
tan(br) y (r) they are not constant multiples of cach other, so they are linearly
independent. Hence by Theorem 1.23, they form a fundamental set of solutions,
and the general solution can be written as
ya) = Ay (1) + A₂y2(1) Ae" cos(ht) + Age sin(br),
where A, and Ay are arbitrary constants.
We summarize our discussion in the following proposition.
Then, differentiate all of them (in their exponential forms) and verify the standard
derivative formulae.
153](https://content.bartleby.com/qna-images/question/5e343f85-ac09-4dac-ae1f-fa90b444949b/1a8321d3-bd84-490a-bb24-2a1fc96c50ac/fsk6upy_processed.jpeg)
Transcribed Image Text:Compica FOOLS
If the roots to the characteristic equation (3.2) are complex,' then, since the coef-
ficients of the characteristic polynomial are real, the roots are complex conjugates.
They have the form λ = a + ib and =a-ib. The corresponding solutions are
z(t) = e(+) and Z(t)=ea-ib. Using Euler's formula, these solutions become
z(t) = (a+b) =
Z(t)=ea-ib
et [cos(br) + i sin(br)]. and
=e" [cos(bt) - i sin(br)].
where
Since (t) = e-22(1), the solutions are not constant multiples of each other, so
they are linearly independent. Hence using Theorem 1.23, we see that the general
solution is
y(t) = C₁z(t) + C₂Z(r).
(3.8)
The solutions and are complex valued. Such solutions are often preferred (for
2
example, in circuit analysis). However, we are aiming for real valued solutions.
Notice from (3.7) that z and Z are complex conjugates. Written in terms of their
real and imaginary parts, we have
2(t)= y(t) +¡y₂(r) and (r) = y(t)-iys(t).
Thus we have
(3.7)
y(t) = Rez(t) = e cos(br) and y(t) = Imz(t) = esin(bt). (3.10)
+3 Linear, Homogeneous Equations with Constant Coefficienta
using complex (or real) exponentials:
sin z, cos 2, tan r, sinh r, cosh 2, tanh r
(3.9)
3) == (20)+2()) and 32(0)= (200)-2010).
Therefore, by Proposition 1.18. y() and y₂(1), the real and imaginary parts of
z(t), are solutions. Furthermore, these are real valued solutions. Since y(t) =
tan(br) y (r) they are not constant multiples of cach other, so they are linearly
independent. Hence by Theorem 1.23, they form a fundamental set of solutions,
and the general solution can be written as
ya) = Ay (1) + A₂y2(1) Ae" cos(ht) + Age sin(br),
where A, and Ay are arbitrary constants.
We summarize our discussion in the following proposition.
Then, differentiate all of them (in their exponential forms) and verify the standard
derivative formulae.
153
Expert Solution
arrow_forward
Step 1
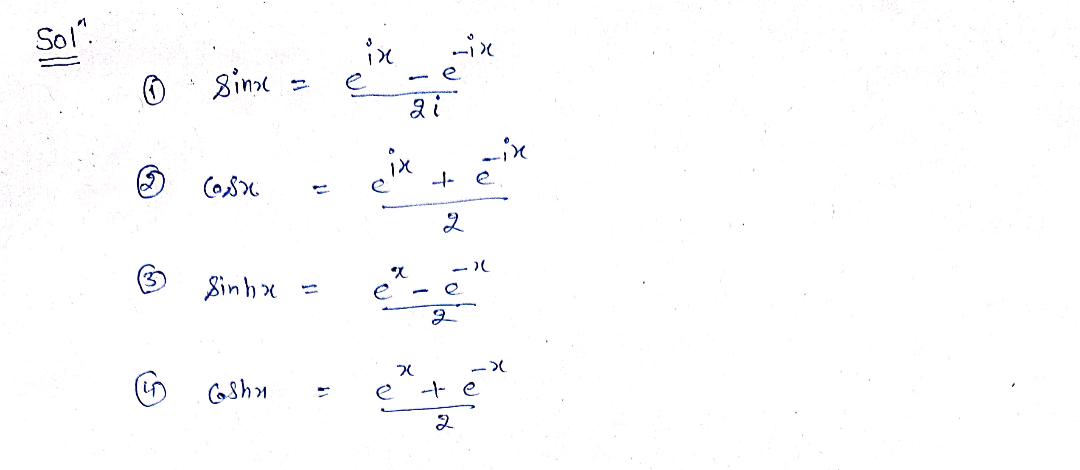
Step by stepSolved in 2 steps with 2 images
Knowledge Booster
Similar questions
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,