
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
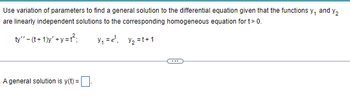
Transcribed Image Text:Use variation of parameters to find a general solution to the differential equation given that the functions and
Y₁
Y₂
are linearly independent solutions to the corresponding homogeneous equation for t> 0.
ty" - (t+1)y'+y=t²; Y₁ = e¹₁ y₂=t+1
A general solution is y(t) = 0.
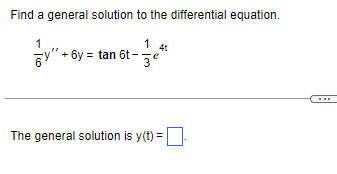
Transcribed Image Text:Find a general solution to the differential equation.
14t
1
y"+6
6t-3
+6y= tan 6t
The general solution is y(t) =
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
- Consider the differential equation x²y" - 9xy' + 24y = 0; x4, x6, (0, ∞). Verify that the given functions form a fundamental set of solutions of the differential equation on the indicated interval. w(x4, x) = The functions satisfy the differential equation and are linearly independent since # 0 Form the general solution. y = for 0 < x < 0,arrow_forwardAn integrating factor for the linear differential equation Y- 2y : = 12x is u= | A. 2xe2x В. — 2 C.-2x D. In 2x O E. e Е. -2xarrow_forwardConsider the function of two variables u (x,t) = 2e-t sin (2x) Select the option that gives a partial differential equation for which this function of two variables is a solution. A. (∂2u/∂x2) = 4(∂2u/∂t2) B. (∂2u/∂x2) = (1/4)(∂2u/∂t2) C. (∂2u/∂x2) = - (1/4)(∂2u/∂t2) D. (∂2u/∂x2) = -4 (∂u/∂t) E. (∂2u/∂x2) = 4 (∂u/∂t)arrow_forward
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

