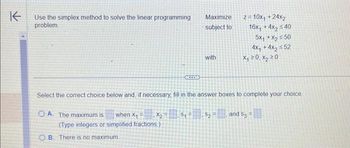
Use the simplex method to solve the linear programming problem. ECOS B. There is no maximum Maximize subject to S₁ F with z=10x₁ +24x₂ Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. OA. The maximum is when x₁ = X₂= and S₂ = (Type integers or simplified fractions) $2 16x, +4x₂ ≤40 5X4+X,550 4x, +4x₂ ≤52 X₁ 20, X₂ 20

August eats a mix of Food X and Food ? Y for lunch. The amount of protein, calories,and sodium per ounce for each is shown in the table below. August's lunch should provide atleast 520 calories but less than or equal to 750 milligrams of sodium. August would like to maximize the amount of protein in his lunch mix. Let ? denote the number of ounces for Food X and let ? denote the number of ounces of Food Y. Topic: Graphical Method