Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
I attached an example of how to solve the problem accordingly. Please follow along. Thank you.
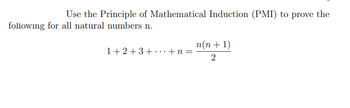
Transcribed Image Text:Use the Principle of Mathematical Induction (PMI) to prove the
following for all natural numbers n.
1+2+3+...+n=
n(n+1)
2
![. Use the Principle of Mathematical Induction (PMI) to prove the
following for all natural numbers n.
• P(1) is
3
P(n)
3+ 11 +19++ (8n — 5) = 4n² — n (neN) Pin)
true
because
4(1)²_1=3 ✓
ころ
is true for some neN.
3 +11 +19+ - • -+ (8n −5)]=4n²_n_P(n)
•Assume P(n)
Need to prove Pin+1)
[3+11+19+---+ (8n - 5] + [8(n+1)-5] pon+1)
=4[n+1]²_[n+i]
Proof of pintl):
3+1+19+...+ (8n_5)+(8n+3)
= 4n²_n +8n-3
=4n²+7n-3
Note: 4[n+1]-[n+1] =4[n²+²n +i]-[n+i]
3
=4n² +8n++-n-1
=4n²+7+3
This proves P(n+l).
•
PMI implies (EN) P(n) is true.
A](https://content.bartleby.com/qna-images/question/d49a5070-9d99-4a2f-a144-be47e7ddead5/da27416d-a80e-41b9-8276-5504262e4843/sut7ayq_processed.png)
Transcribed Image Text:. Use the Principle of Mathematical Induction (PMI) to prove the
following for all natural numbers n.
• P(1) is
3
P(n)
3+ 11 +19++ (8n — 5) = 4n² — n (neN) Pin)
true
because
4(1)²_1=3 ✓
ころ
is true for some neN.
3 +11 +19+ - • -+ (8n −5)]=4n²_n_P(n)
•Assume P(n)
Need to prove Pin+1)
[3+11+19+---+ (8n - 5] + [8(n+1)-5] pon+1)
=4[n+1]²_[n+i]
Proof of pintl):
3+1+19+...+ (8n_5)+(8n+3)
= 4n²_n +8n-3
=4n²+7n-3
Note: 4[n+1]-[n+1] =4[n²+²n +i]-[n+i]
3
=4n² +8n++-n-1
=4n²+7+3
This proves P(n+l).
•
PMI implies (EN) P(n) is true.
A
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 3 images
Knowledge Booster
Similar questions
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,