
Elements Of Electromagnetics
7th Edition
ISBN: 9780190698614
Author: Sadiku, Matthew N. O.
Publisher: Oxford University Press
expand_more
expand_more
format_list_bulleted
Question
Please check if it’s correct
![Use the middle of the 5 measurements for your calculations. Use the equation:
\[ a = g \sin(\theta) \]
to find the acceleration due to gravity. Of course you'll need the equations of kinematics to determine the acceleration "a" first before finding \( g \). Again compare your result to the actual value of 9.80 m/sec\(^2\).
Then list 5 possible reasons why your result was different than the expected value.](https://content.bartleby.com/qna-images/question/560885b1-95a6-46a1-8479-9132da42c8bd/619a0bd6-3ad5-4e07-a786-5027053f92a5/0zbch_thumbnail.jpeg)
Transcribed Image Text:Use the middle of the 5 measurements for your calculations. Use the equation:
\[ a = g \sin(\theta) \]
to find the acceleration due to gravity. Of course you'll need the equations of kinematics to determine the acceleration "a" first before finding \( g \). Again compare your result to the actual value of 9.80 m/sec\(^2\).
Then list 5 possible reasons why your result was different than the expected value.

Transcribed Image Text:**Experiment #2**
In this section of the experiment, we will locate a smooth surface at an angle and measure the distance between the starting and finishing points of the hill. Then we'll place a ball at the top of the hill, let it go, and time how long it takes for the ball to roll down the hill, and repeat until we get 5 measurements total.
**Diagram and Calculations:**
1. **Triangle Setup:**
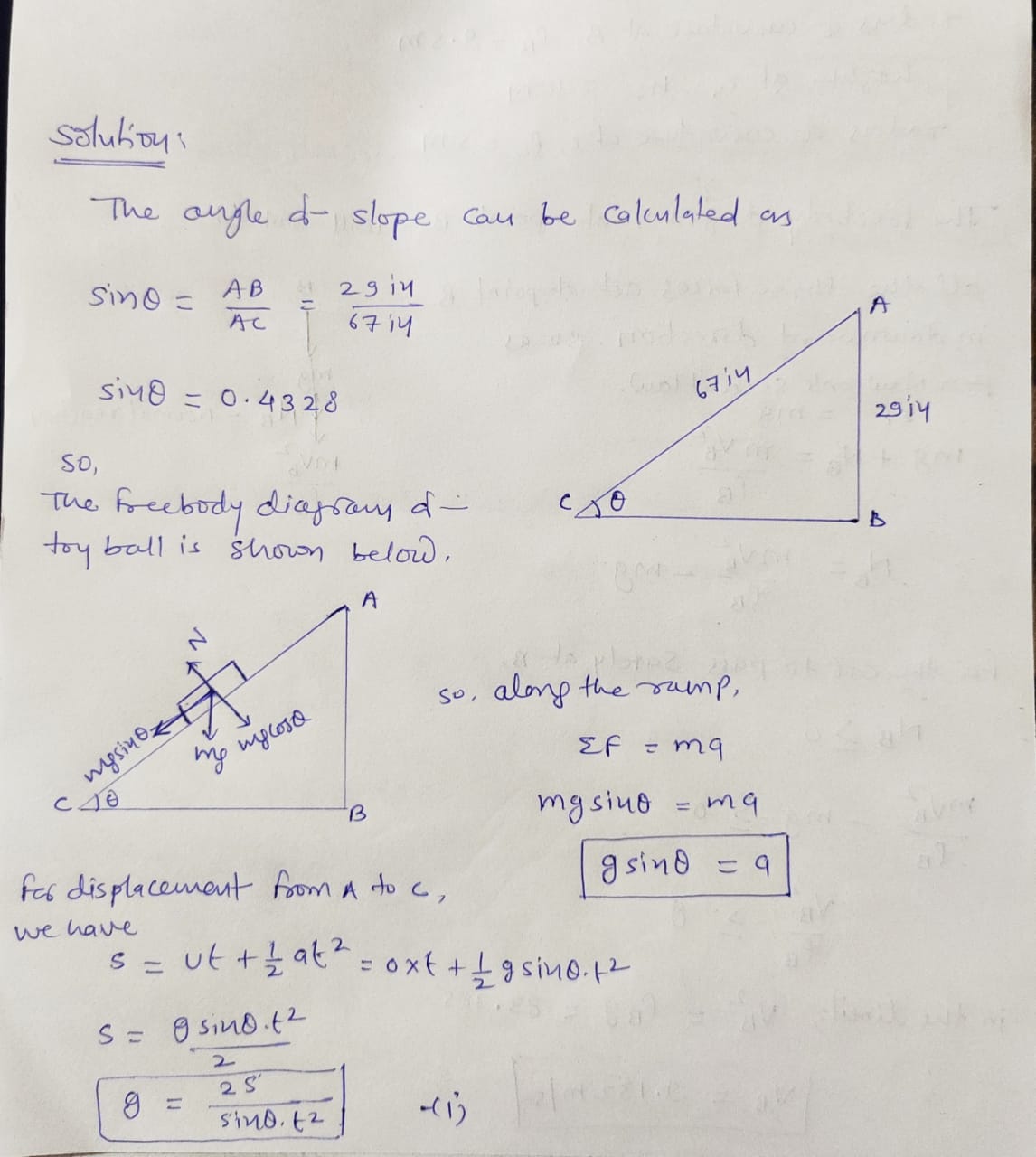
- Triangle ABC with:
- \( AB = 29 \text{ in} \)
- \( AC = 67 \text{ in} \)
- \(\sin \theta = \frac{AB}{AC} = \frac{29}{67} = 0.4328\)
- \(\theta = \sin^{-1}(0.4328) \approx 25.6^\circ\)
2. **Kinematic Equation:**
- Given:
- \(a = g \sin \theta\)
- \(u = 0\)
- Equation:
- \( s = ut + \frac{1}{2} at^2 \)
- \( s = \frac{1}{2} g \sin \theta t^2 \)
- \( g = \frac{2s}{\sin \theta t^2} \)
3. **Time of Top Going Down Hill:**
| Trial | Time (sec) |
|-------|------------|
| 1 | 0.80 sec |
| 2 | 0.60 sec |
| 3 | 0.74 sec |
| 4 | 0.46 sec |
| 5 | 0.66 sec |
4. **Average Time and Calculations:**
- Average time \( t = \frac{0.74 + 0.84 + 0.46 + 0.66}{5} = 0.5 \text{ sec} \)
- Distance \( s = 67 \text{ in} = 1.7018 \text{ m} \)
- \(\sin \theta = 0.4328\)
- \( g = \frac{s}{\sin \theta t^2} = \frac{2(1.7018)(0.5^2)}{
Expert Solution
arrow_forward
Step 1
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- What is the diameter of the groove?arrow_forwardI am going to use a Bolt through the .41 DIA holes to align the parts, answer the following:What is the Bolt size (don't worry about the tolerances)?Dim's C=.75, B=2.50, apply a +/-.01 tol to all affected dim's except the .50+/-.03 dim, how far does EDGE D stick out above EDGE E (figure it off the centerline, don't worry abou the clearance between the bolt and the holes)?Min = ? Max= ?arrow_forwardThe torque is incorrect please solve for torquearrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY

Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press

Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON

Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education

Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY

Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning

Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY