Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
(36) Use the identity 1∕(k(k + 1)) = 1∕k − 1∕(k + 1) and Exercise 35 to compute ∑n 1∕(k(k + 1)).
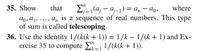
Transcribed Image Text:**Transcription for Educational Website**
**Mathematics Exercise: Telescoping Sums**
**Exercise 35:**
Show that the sum \(\sum_{j=1}^{n} (a_j - a_{j-1}) = a_n - a_0\), where \(a_0, a_1, \ldots, a_n\) is a sequence of real numbers. This type of sum is called *telescoping*.
**Exercise 36:**
Use the identity \(1/(k(k+1)) = 1/k - 1/(k+1)\) and apply Exercise 35 to compute \(\sum_{k=1}^{n} 1/(k(k+1))\).
**Discussion:**
In Exercise 35, the concept of telescoping sums is explored. A telescoping sum is one where consecutive terms cancel each other out, leaving only the first and last elements in the sequence. The result is a simplified expression involving only the initial and final terms of the sequence.
In Exercise 36, you are asked to apply this concept using a given identity. The identity simplifies the terms so that they telescope, allowing for easy calculation of the sum from \(k=1\) to \(n\) for the expression \(1/(k(k+1))\).
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images
Knowledge Booster
Similar questions
- find f prime of xarrow_forwardb) J(x) = 2x 5-4t t 40)=128 If h(t)= 7x+3, X -3 f(x) -1 tale , evaluate h(4-1³). Use the table to fill in the missing values. Th a) f(1) 35 0 3 b) f( 1 -1 -1 -4arrow_forwardShow that for all real values of x, [(x-2)(x-4)] / 4x - 7 cannot take values between -1 and -1/4 Given that x is real and that x ≠ 2. show that g(x) = x2/(x-2) cannot take values Between 0 and 8 .arrow_forward
- Find the expression of Px²9x²(x +t), pxμ(x + t) with steps, if s(x +t) = s(x)(1-t) s(x + 1)t (Exponential Interpolation Assumption of Fractional Ages)arrow_forwardI need the answer as soon as possiblearrow_forward[1 1 [A]{X} = {b} Where [A] 1 2 If 1 and l2 1 -1 (X1) {b} = }1}. Find {X}: X2 (x3) Select one: a. {X} = {X2 = (X1) O b. {X} = }X2 = (x3) (X1 X2 (x3) O c. {X} = {5 O d. {X} = }X2 O e. None of these 花为arrow_forward
- d.x 1 (g) Explain why x(x + 1) k(k +1) k=1arrow_forwardShow that an equation x³ -x-1=0 can be written as follows: 1 x²-1 (a) (b) x=1+ =g₁(x) X x²+x+1 -=8₂(x) Forg, and g₂ do iteration up to three steps starting with x = 1.5. Based on the result, decide the best expression for g and approximate the root.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,