
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Question
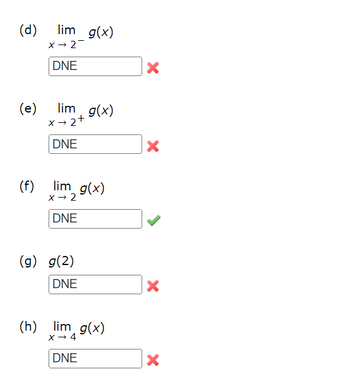
Transcribed Image Text:### Understanding Limits and Function Values: Examples and Exercises
#### Example Problems and Solutions:
**(d) \(\lim_{x \to 2^{-}} g(x)\)**
Given value: **DNE (Does Not Exist)**
Status: ❌ Incorrect
---
**(e) \(\lim_{x \to 2^{+}} g(x)\)**
Given value: **DNE (Does Not Exist)**
Status: ❌ Incorrect
---
**(f) \(\lim_{x \to 2} g(x)\)**
Given value: **DNE (Does Not Exist)**
Status: ✅ Correct
---
**(g) \(g(2)\)**
Given value: **DNE (Does Not Exist)**
Status: ❌ Incorrect
---
**(h) \(\lim_{x \to 4} g(x)\)**
Given value: **DNE (Does Not Exist)**
Status: ❌ Incorrect
---
### Explanation:
#### Understanding Limits:
1. **One-Sided Limits:**
- \(\lim_{x \to a^{-}} f(x)\) refers to the limit of \(f(x)\) as \(x\) approaches \(a\) from the left (less than \(a\)).
- \(\lim_{x \to a^{+}} f(x)\) refers to the limit of \(f(x)\) as \(x\) approaches \(a\) from the right (greater than \(a\)).
2. **Two-Sided Limits:**
- \(\lim_{x \to a} f(x)\) refers to the limit of \(f(x)\) as \(x\) approaches \(a\) from both sides. This limit exists if and only if both one-sided limits exist and are equal.
3. **Function Value:**
- \(f(a)\) refers to the actual value of the function at \(x = a\).
#### Common Scenarios where Limits Do Not Exist (DNE):
1. If the left-hand limit and the right-hand limit are not equal.
2. If the function approaches infinity or negative infinity as \(x\) approaches the specified point.
3. If the function exhibits oscillatory behavior (e.g., \( \sin(\frac{1}{x}) \) as \(x\) approaches 0).
In these examples, the responses given for parts (d), (
![### Calculating Limits Using a Graph
To determine the value of each limit using the graph of \( g \), observe the behavior of \( g \) as \( x \) approaches the specified value. If an answer does not exist, enter DNE.
#### Graph Description:
- **Axes**: The graph features a Cartesian coordinate system with the \( x \)-axis ranging from \( -2 \) to \( 6 \) and the \( y \)-axis ranging from \( -4 \) to \( 6 \).
- **Curve of \( g \)**: The curve \( g \) has the following notable points:
- A closed dot at \( (-2, -2) \)
- An open circle at \( (0, -1) \)
- A closed dot at \( (2, 1) \)
- An open circle at \( (3, 1.5) \)
- A closed dot at \( (4, 2) \)
- An open circle at \( (5, 2.5) \)
- **Behavior**:
- **Near \( x = 0 \)**: As \( x \) approaches 0 from the left, the value of \( g(x) \) approaches \( -1 \). Similarly, as \( x \) approaches 0 from the right, the value of \( g(x) \) also approaches \( -1 \).
#### Problems and Solutions:
(a) \[
\lim_{{x \to 0^-}} g(x)
\]
Looking at the graph from the left of \( x = 0 \), the function \( g(x) \) approaches \( -1 \) as \( x \) approaches \( 0 \).
**Answer**: \[
\lim_{{x \to 0^-}} g(x) = -1
\]
(b) \[
\lim_{{x \to 0^+}} g(x)
\]
Looking at the graph from the right of \( x = 0 \), the function \( g(x) \) also approaches \( -1 \) as \( x \) approaches \( 0 \).
**Answer**: \[
\lim_{{x \to 0^+}} g(x) = -1
\]
(c) \[
\lim_{{x \to 0}} g(x)
\]
Since both one](https://content.bartleby.com/qna-images/question/00067d91-5c79-4b53-8e03-40299a52da99/6be6f97c-15b7-4ce6-8b18-e940bee42873/ikndyzl_thumbnail.png)
Transcribed Image Text:### Calculating Limits Using a Graph
To determine the value of each limit using the graph of \( g \), observe the behavior of \( g \) as \( x \) approaches the specified value. If an answer does not exist, enter DNE.
#### Graph Description:
- **Axes**: The graph features a Cartesian coordinate system with the \( x \)-axis ranging from \( -2 \) to \( 6 \) and the \( y \)-axis ranging from \( -4 \) to \( 6 \).
- **Curve of \( g \)**: The curve \( g \) has the following notable points:
- A closed dot at \( (-2, -2) \)
- An open circle at \( (0, -1) \)
- A closed dot at \( (2, 1) \)
- An open circle at \( (3, 1.5) \)
- A closed dot at \( (4, 2) \)
- An open circle at \( (5, 2.5) \)
- **Behavior**:
- **Near \( x = 0 \)**: As \( x \) approaches 0 from the left, the value of \( g(x) \) approaches \( -1 \). Similarly, as \( x \) approaches 0 from the right, the value of \( g(x) \) also approaches \( -1 \).
#### Problems and Solutions:
(a) \[
\lim_{{x \to 0^-}} g(x)
\]
Looking at the graph from the left of \( x = 0 \), the function \( g(x) \) approaches \( -1 \) as \( x \) approaches \( 0 \).
**Answer**: \[
\lim_{{x \to 0^-}} g(x) = -1
\]
(b) \[
\lim_{{x \to 0^+}} g(x)
\]
Looking at the graph from the right of \( x = 0 \), the function \( g(x) \) also approaches \( -1 \) as \( x \) approaches \( 0 \).
**Answer**: \[
\lim_{{x \to 0^+}} g(x) = -1
\]
(c) \[
\lim_{{x \to 0}} g(x)
\]
Since both one
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning