
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
thumb_up100%
![**Problem Statement:**
Use Laplace transforms to solve the following initial value problem.
\[ x'' + 4x' + 13x = te^{-t} \]
Initial conditions:
- \( x(0) = 0 \)
- \( x'(0) = 4 \)
**Solution:**
\[ x(t) = \ldots \] (Solution to be determined using Laplace transforms)](https://content.bartleby.com/qna-images/question/3200e892-7b83-4670-8aa5-c4c84f2a6adb/2e19edb2-4be7-488b-be43-06333d2e864c/viyl72o_thumbnail.png)
Transcribed Image Text:**Problem Statement:**
Use Laplace transforms to solve the following initial value problem.
\[ x'' + 4x' + 13x = te^{-t} \]
Initial conditions:
- \( x(0) = 0 \)
- \( x'(0) = 4 \)
**Solution:**
\[ x(t) = \ldots \] (Solution to be determined using Laplace transforms)
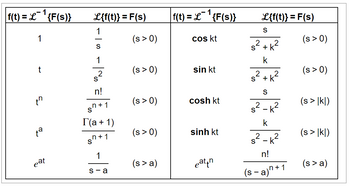
Transcribed Image Text:## Laplace Transform Pairs
The table below provides a list of common Laplace transforms and their inverse transforms, useful for various applications in engineering and physics.
### Laplace Transform Formulas
#### Left Side: Basic Functions
1. **Constant Function (1):**
- \( f(t) = 1 \Rightarrow \mathcal{L}\{f(t)\} = \frac{1}{s} \quad (s > 0) \)
2. **Linear Function (t):**
- \( f(t) = t \Rightarrow \mathcal{L}\{f(t)\} = \frac{1}{s^2} \quad (s > 0) \)
3. **Power Function (\(t^n\)):**
- \( f(t) = t^n \Rightarrow \mathcal{L}\{f(t)\} = \frac{n!}{s^{n+1}} \quad (s > 0) \)
4. **General Power Function (\(t^a\)):**
- \( f(t) = t^a \Rightarrow \mathcal{L}\{f(t)\} = \frac{\Gamma(a+1)}{s^{n+1}} \quad (s > 0) \)
5. **Exponential Function (\(e^{at}\)):**
- \( f(t) = e^{at} \Rightarrow \mathcal{L}\{f(t)\} = \frac{1}{s-a} \quad (s > a) \)
#### Right Side: Trigonometric and Hyperbolic Functions
1. **Cosine Function (\(\cos kt\)):**
- \( f(t) = \cos kt \Rightarrow \mathcal{L}\{f(t)\} = \frac{s}{s^2 + k^2} \quad (s > 0) \)
2. **Sine Function (\(\sin kt\)):**
- \( f(t) = \sin kt \Rightarrow \mathcal{L}\{f(t)\} = \frac{k}{s^2 + k^2} \quad (s > 0) \)
3. **Hyperbolic Cosine Function (\(\cosh kt\)):**
- \( f(t) = \cosh kt \Rightarrow \mathcal{L}\{f
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps with 5 images

Knowledge Booster
Similar questions
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

