
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
thumb_up100%
Pls help on these two questions. PLS I BEG DO BOTH OF THEM.

Transcribed Image Text:Use Laplace transform to solve the following initial value problem
y" + 4y = 4, y(0) = –5, y'(0) = –4
Express your answer as the Laplace transform of y and use partial fraction decomposition where possible.
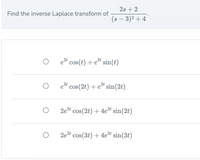
Transcribed Image Text:2s + 2
Find the inverse Laplace transform of
(s – 3)2 + 4
est cos(t) + et sin(t)
e* cos(2t) + e* sin(2t)
2et cos(2t) + 4et sin(2t)
2et cos(3t) + 4et sin(3t)
Expert Solution
arrow_forward
Step 1
Given differential equation is and
We have to solve the given initial value problem by using Laplace transformation.
Use and
Now, use Laplace transform of both side in
Hence,
Now, taking a pretrial fraction of , which is given below
And taking a pretrial fraction of , which is given below
Therefore,
Now, taking inverse Laplace transform, which is given below
Hence,
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- please answer the questions i sent, exactly in the form of the question thank you so mucharrow_forwardQuestion: Why 1 divided by 0.5 = 2? 1 cookie divided by two people, each get 1/2 of the cookie. 2 cookies divided by two people, each get 1 of the cookie. 1 cookie divded by 0.5 people, each get 2 cookies? It seems doesnt make sense. Explain with this exmaple.arrow_forwardSubtract. 2 27 3 4 3 2 (Simplify your answer.) 27 4 IIarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

