Question
Use Kirchhoff’s rules to calculate the current in each branch. Assume that each resistor has a resistance of 100 Ω and that V1 = 9 V and V2 = 12 V.
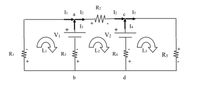
Transcribed Image Text:R2
I2
I c Is
a
I3
I4
+
V1
V2
RI
R3
R4
Rs
b
d
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
- Consider the circuit shown in the figure below. (Assume R1 = 12.0 Ω and R2 = 6.50 Ω.) (a) Find the potential difference between points a and b. (b) Find the current in the 20.0-Ω resistor. Aarrow_forwardA 22 Ω resistor and a 4 Ω resistor are connected in series to an ideal 12 V battery.Find the current in each resistor.Answer in units of A.Find the potential difference across the firstresistor.Answer in units of V.Find the potential difference across the secondresistor.Answer in units of V.arrow_forwardFour resistors (R1=6 ohms, R2=5 ohms, R3= 4 ohms, R4=34 ohms) are connected in parallel. Find the current in R2 if the total voltage is 220 Varrow_forward
- Using Kirchhoff's rules, find the following. (&₁ = 70.2 V, &2 = 61.4 V, and 83 78.6 V.) = 4.00 ΚΩ = = b = Es a IR3 2.00 ΚΩ (a) the current in each resistor shown in the figure above X IRI Apply Kirchhoff's rules to write a set of simultaneous equations that can be solved for the current in each part of the circuit. mA X R₂ R₁ E₂ R3 f 3.00 ΚΩ d E₂ 3 R2 Apply Kirchhoff's rules to write a set of simultaneous equations that can be solved for the current in each part of the circuit. mA X Apply Kirchhoff's rules to write a set of simultaneous equations that can be solved for the current in each part of the circuit. mAarrow_forwardFind the currents I1 and I2, and the current through the battery, I. Find the equivalent resistance of the circuit.arrow_forwardMultiple-Concept Example 9 discusses the physics principles used in this problem. Three resistors, 1.18, 3.31, and 3.860, are connected in series across a 28.3-V battery. Find the power delivered to each resistor.arrow_forward
- Problem 2: The battery has a potential difference of 10 V and each resistor has a resistance of 2 ohms. RI R2 'R3 (a) Determine the equivalent resistance of the 3 resistors. (i.e. if you replace the three resistors shown with a single equivalent resistor, what value should you select?) 3 ohms (b) Determine the current through each resistor. (R1 has 1.66 A, R2 has 1.66 A, R3 has 3.33A)arrow_forwardConsider the following circuit diagram. The potential difference across the battery is 40.0 volts, and it supplies a current of 5.00 amperes to the circuit. There is a current of of 2.70 amperes flowing through R1. Resistor R2 has a resistance of 5.50 ohms. What is the resistance of R3? Answer in ohms to two decimal places, but do not include units in your answer.arrow_forwardResistance, R, is defined using R = V/I where V is the potential across a resistor, and I is thecurrent. R is measured in ohms (Ω), where 1 Ω = 1 V/A. The constant you determined in eachequation should be similar to the resistance of each resistor. However, resistors aremanufactured such that their actual value is within a tolerance. For many common resistors, thetolerance is 5% or 10%. Calculate the range of possible values for each resistor. Does the constant in each equation fit within the appropriate range of values for each resistor? Do the resistors follow Ohm’s law? Base your answer on your experimental data. Slope (V/A) Y-intercept (V) Resistor 10 Ω 9.896V/A 0.0005526V Resistor 51 Ω 50.91V/A 0.01030V Light bulb (first 3 pts) 5.386V/A n/a Light bulb (last 10 pts) 43.26V/A n/aarrow_forward
- The circuit below contains two real batteries, each having significant internal resistance. Battery #1 has an EMF of 6.00 V and an internal resistance of 1.00 ohm. Battery #2 has an EMF of 12.00 V and an internal resistance of 2.00 ohms. These two batteries are connected in series with two resistors R, = 6.00 ohms and R,= 3.00 ohms. ri d (6.00,V) (1.00 0) R1 (6.00 N) R2 (3.00 N) a r2 E2 (2.00 Q) (12.00 V) 18. The current in the 12.00 Volt battery is equal to C. 0.500 A. A. 0.750 A. B. 1.00 A. D. 2.00 A. E. 1.50 A. 19. The potential difference across the terminals of battery #1 from point C to point d is equal to C. 7.00 V. A. 5.50 V. B. 6.00 V. D. 5.00 V. E. 6.50 V. 20. The potential difference across the terminals of battery #2 from point a to point b is equal to C. 13.00 V. A. 14.00 V. В. 10.00 V. D. 11.0 V. E. 12.00 V.arrow_forwardThe figure shows a resistor of resistance R = 6.102 connected to an ideal battery of emf 8 = 15.4 V by means of two copper wires. Each wire has length 21.4 cm and radius 2.20 mm. In dealing with such circuits in this chapter, we generally neglect the potential differences along the wires and the transfer of energy to thermal energy in them. Check the validity of this neglect for the circuit of the figure below. What is the potential difference across (a) the resistor and (b) each of the two sections of wire? At what rate is energy lost to thermal energy in (c) the resistor and (d) each section of wire? 8=1 Wire 1 R Wire 2arrow_forward
arrow_back_ios
arrow_forward_ios