Understanding the Application of Probability to Genetics A couple has 6 children. a.) What is the probability the first child will be a boy and the rest girls? b.) Which combination of boys and girls would have the greatest number of combinations and therefore the highest probability of occurrence?

Event: In probability theory, an event is an outcome or a set of outcomes of a random experiment to which a probability is assigned. A single outcome is an element of a sample space and different events in a random experiment are generally not equally likely, since they may include very different groups of outcomes.
Independent Events: A number of events are said to be independent if the probability of occurrence of any one of them is not affected by the supplementary information regarding the occurrence of any number of the remaining events.
Let there are n independent events A1, A2, ... , An with P(Ai) > 0 for all i = 1, 2, ... , n. Then we have,
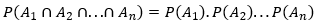
Combination: A combination is a selection of items from a group of items, where the order of selection is not taken into consideration.
For example, let us suppose there are three balls viz. a red, a green and a blue. From these, there are three combinations of two balls that can drawn from this set. The combinations are a red and a green ball, a green and a blue ball and a blue and a red ball.
Mathematically, the number of combinations of r items drawn from a set of n distinct items is given by the binomial coefficient
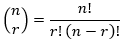
Step by step
Solved in 3 steps with 2 images




