Two tanks, each holding 100 L of liquid, are interconnected by pipes with liquid flowing from tank A into tank B at a rate of 12 L/min and from tank B into tank A at 3 L/min, as shown in the figure. The liquid inside each tank is kept well stirred. Pure water flows into tank A at a rate of 9 L/min, and the solution flows out of tank B at 9 L/min. If, initially, tank A contains 2.6 kg of salt and tank B contains no salt (only water), determine the mass of salt in each tank at time t≥ 0. Graph on the same axes the two quantities x₁ (t) and x₂ (t), where x₁ (t) is the mass of salt in tank A and x₂(t) is the mass in tank B. Click the icon to view the figure of the tanks. X What are the equations for the mass of salt in each tank at time t≥ 0? X₁ (t)= X₂ (t) = Tanks 9 L/min Pure water A x₁ (1) 100 L x₁ (0)=2.6 kg Print 12 L/min 3 L/min B x₂ (1) 100 L x₂(0)=0 kg Done 9 L/min Q Q
Two tanks, each holding 100 L of liquid, are interconnected by pipes with liquid flowing from tank A into tank B at a rate of 12 L/min and from tank B into tank A at 3 L/min, as shown in the figure. The liquid inside each tank is kept well stirred. Pure water flows into tank A at a rate of 9 L/min, and the solution flows out of tank B at 9 L/min. If, initially, tank A contains 2.6 kg of salt and tank B contains no salt (only water), determine the mass of salt in each tank at time t≥ 0. Graph on the same axes the two quantities x₁ (t) and x₂ (t), where x₁ (t) is the mass of salt in tank A and x₂(t) is the mass in tank B. Click the icon to view the figure of the tanks. X What are the equations for the mass of salt in each tank at time t≥ 0? X₁ (t)= X₂ (t) = Tanks 9 L/min Pure water A x₁ (1) 100 L x₁ (0)=2.6 kg Print 12 L/min 3 L/min B x₂ (1) 100 L x₂(0)=0 kg Done 9 L/min Q Q
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
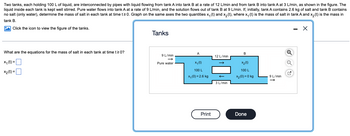
Transcribed Image Text:**Problem Statement:**
Two tanks, each holding 100 L of liquid, are interconnected by pipes with liquid flowing from tank A into tank B at a rate of 12 L/min and from tank B into tank A at 3 L/min, as shown in the figure. The liquid inside each tank is kept well stirred. Pure water flows into tank A at a rate of 9 L/min, and the solution flows out of tank B at 9 L/min. If, initially, tank A contains 2.6 kg of salt and tank B contains no salt (only water), determine the mass of salt in each tank at time \( t \geq 0 \). Graph on the same axes the two quantities \( x_1(t) \) and \( x_2(t) \), where \( x_1(t) \) is the mass of salt in tank A and \( x_2(t) \) is the mass in tank B.
**Diagram Explanation:**
- **Tanks Diagram:**
- **Tank A:**
- Input: 9 L/min of pure water
- Internal flow: 12 L/min to Tank B
- Initial salt mass: \( x_1(0) = 2.6 \) kg
- **Tank B:**
- Input: 12 L/min from Tank A and 3 L/min back to Tank A
- Output: Tank B outputs solution at 9 L/min
- Initial salt mass: \( x_2(0) = 0 \) kg
**Questions:**
What are the equations for the mass of salt in each tank at time \( t \geq 0 \)?
- \( x_1(t) = \)
- \( x_2(t) = \)
**Note:**
The diagram is included to assist in understanding the flow of liquids and the initial conditions in each tank. It shows the rates of flow and the initial amount of salt present, providing a visual representation to support the problem requirements.
Expert Solution
Step 1: Evaluation of eigenvalues and eigenvectors
Step by step
Solved in 3 steps with 4 images
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
