Two stacked boxes are sliding along an ice rink with an initial velocity vo to the right. You are trying to stop the boxes so you exert a force Fy1 on the top box as indicated in the figure. F V. 1 2 The magnitude of the force that you exert is variable, and follows the equation: Fy1 Fo e - bt with Fo and b constants, and t the time since you began exerting the force. Because the boxes are sliding on ice, the friction between box 2 and the ground is negligible. There is friction between the two boxes, and they are observed to accelerate together as you exert the force to slow them down. Note: This problem will be much easier if you solve everything symbolically before you substitute numerical values for the parameters. Use the following values for the parameters: mị = 9 kg то — 4 kg $ = 30.7° Fo = 99 N b= 0.18 s¬1 tį = 3.1 s Yn = 9,8 m/s
Two stacked boxes are sliding along an ice rink with an initial velocity vo to the right. You are trying to stop the boxes so you exert a force Fy1 on the top box as indicated in the figure. F V. 1 2 The magnitude of the force that you exert is variable, and follows the equation: Fy1 Fo e - bt with Fo and b constants, and t the time since you began exerting the force. Because the boxes are sliding on ice, the friction between box 2 and the ground is negligible. There is friction between the two boxes, and they are observed to accelerate together as you exert the force to slow them down. Note: This problem will be much easier if you solve everything symbolically before you substitute numerical values for the parameters. Use the following values for the parameters: mị = 9 kg то — 4 kg $ = 30.7° Fo = 99 N b= 0.18 s¬1 tį = 3.1 s Yn = 9,8 m/s
Related questions
Question
I am unsure how to really start this problem. How would I set this up?
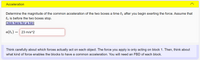
Transcribed Image Text:Acceleration
Determine the magnitude of the common acceleration of the two boxes a time ti after you begin exerting the force. Assume that
ti is before the two boxes stop.
Click here for a hint
a(tı) = 23 m/s^2
Think carefully about which forces actually act on each object. The force you apply is only acting on block 1. Then, think about
what kind of force enables the blocks to have a common acceleration. You will need an FBD of each block.
Transcribed Image Text:Two stacked boxes are sliding along an ice rink with an initial velocity vo to the right. You are trying to stop the boxes so you exert a
force Fy1 on the top box as indicated in the figure.
F
Y1
1
2
The magnitude of the force that you exert is variable, and follows the equation: Fy1 = Fo e
- bt
with Fo and b constants, and t the time
since you began exerting the force.
Because the boxes are sliding on ice, the friction between box 2 and the ground is negligible. There is friction between the two boxes,
and they are observed to accelerate together as you exert the force to slow them down.
Note: This problem will be much easier if you solve everything symbolically before you substitute numerical values for the parameters.
Use the following values for the parameters:
mị = 9 kg
то — 4 kg
0 = 30.7°
Fo = 99 N
b = 0.18 s-1
t1 = 3.1 s
vg = 9.8 m/s
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 1 images
