Question
In unit vector notation, what is the velocity of the motorist with respect to the police car? and what is the angle between the velocity found and the displacement vector from the police car to the motorist
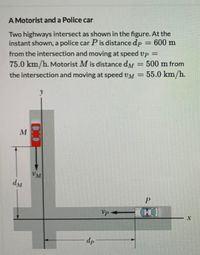
Transcribed Image Text:### A Motorist and a Police Car
Two highways intersect as shown in the figure. At the instant shown, a police car \( P \) is distance \( d_P = 600 \, \text{m} \) from the intersection and moving at speed \( v_P = 75.0 \, \text{km/h} \). Motorist \( M \) is distance \( d_M = 500 \, \text{m} \) from the intersection and moving at speed \( v_M = 55.0 \, \text{km/h} \).
#### Description of Diagram:
- The diagram shows two perpendicular highways crossing each other, forming an intersection.
- A red car, designated as motorist \( M \), is depicted on the vertical highway above the intersection.
- \( M \) is moving downward towards the intersection at a speed of \( v_M = 55.0 \, \text{km/h} \).
- \( M \) is currently \( d_M = 500 \, \text{m} \) away from the intersection.
- A police car, designated as \( P \), is depicted on the horizontal highway to the right of the intersection.
- \( P \) is moving leftward toward the intersection at a speed of \( v_P = 75.0 \, \text{km/h} \).
- \( P \) is currently \( d_P = 600 \, \text{m} \) away from the intersection.
- The intersection itself is the point where both cars' paths would meet if they continue their respective trajectories. The diagram includes axes labeled \( x \) and \( y \), representing the horizontal and vertical directions respectively.
This setup typically helps in analyzing relative motion, interception point calculations, or determining the time it might take for both vehicles to reach the intersection.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 3 images

Knowledge Booster
Similar questions
- What is the angle above the x-axis (north of east) for a vector with components (15 m, 8 m)?arrow_forwardA given line is described by the equation: y = x-l. Vector A starts at point P1 = (0,3) and ends at point P2 on the line such that A is orthogonal to the line. Find an expression for A.arrow_forwardYou have two vectors, A and B such that = 6.4 cm at an angle of 15.8° B = = 2.0 cm at an angle of 83.1° What is the magnitude (in cm) of the vector à + B?arrow_forward
- A vector has an x-component of +5 m and makes an angle of 30° with the + x axis. What is its y-component?arrow_forwardThe x component of vector A is 8.7 units, and its y component is -6.5 units. What is the magnitude of A?arrow_forwardWhich of the following could not be the magnitude of the vector sum of a 25-meter displacement vector and a 35-meter displacement vector? O 15 m O 5 m O 60 m O 10 marrow_forward
- what are the magnitude and angle of a vector with these components? Bx= 7.8 m and By= 10.2 marrow_forwardGiven the vector techniques you worked on in the lab, answer the follow question: suppose you first walk 12 m in a direction 20° west of north, then 20 m in a direction 40° south of west, then 14 m in a direction 30° east of north, and finally 19 m in a direction 40° east of south. How far are you (as the crow flies) from your starting point, and what is the compass direction (west of south) of a line connecting your starting point to your final position?arrow_forwardSydney, Tayler and I go out for a short walk together. We first walked 10 meters 34° South of East, then 20 meters due South, and then 15 meters 42° South of West. We want to find the overall resultant vector of our total travels.arrow_forward
- A treasure hunter following a map walks 11 meters south, 9 meters east, 2 meters north, and 4 meters west. Find the (x,y) coordinates of the treasure hunter’s displacement, and the magnitude of the displacement vector.arrow_forwardDetermine the x and y components of the following three vectors in the xy plane. (a) A 6-m displacement vector that makes an angle of 34° clockwise from the +y direction. x: m y: m (b) A 29-m/s velocity vector that makes an angle of 39° counterclockwise from the -x direction. x: m/s y: m/sarrow_forwardVector A has a magnitude of 15.5 and its direction is 320° counter-clockwise from the +x-axis. What are the x- and y-components of the vector? Ax = Ayarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios