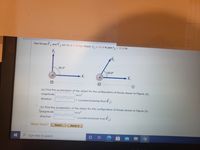
**Title: Understanding Forces and Acceleration****Introduction**In this exercise, we explore how different force configurations affect the acceleration of an object. We will analyze the forces acting on a 2.20-kg object and calculate its resulting acceleration in two scenarios.**Force Configurations**- **Figure (a) Configuration:** - Two forces, \(\vec{F}_1\) and \(\vec{F}_2\), are applied to the object. - \(\vec{F}_1 = 25.0 \, \text{N}\) acts horizontally to the right. - \(\vec{F}_2 = 12.0 \, \text{N}\) acts vertically upward. - The angle between \(\vec{F}_1\) and \(\vec{F}_2\) is \(90.0^\circ\).- **Figure (b) Configuration:** - Again, two forces \(\vec{F}_1\) and \(\vec{F}_2\) are applied. - \(\vec{F}_1 = 25.0 \, \text{N}\) acts horizontally to the right. - \(\vec{F}_2 = 12.0 \, \text{N}\) acts at an angle of \(60.0^\circ\) above the horizontal to the right.**Tasks**- **(a) Calculate the acceleration for Figure (a):** - Determine the magnitude and direction of acceleration with the forces configured as shown.- **(b) Calculate the acceleration for Figure (b):** - Determine the magnitude and direction of acceleration with the forces configured as shown.**Instructions for Solving:**1. **Use Newton's Second Law**: \(\sum \vec{F} = m \vec{a}\), where \(m\) is the mass, and \(\sum \vec{F}\) is the vector sum of forces.2. **Resolve Forces**: Break down the forces into their components if necessary (especially for Figure b).3. **Calculate Acceleration**: - Compute the net force from the force components. - Determine the magnitude of the acceleration using \(a = \frac{F_{\text{net}}}{m}\). - Use trigonometry to find the direction of the acceleration.**Assistance:**- If

Name: **Title: Understanding Forces and Acceleration****Introduction**In th
Uploaded: 2024-03-20T06:56:46.000Z
Channel: Bartleby
Description: **Title: Understanding Forces and Acceleration****Introduction**In this exercise, we explore how different force configurations affect the acceleration of an object. We will analyze the forces acting on a 2.20-kg object and calculate its resulting a

Newton's second law of motion states that the net force acting on a system produces an acceleration…

Science

Physics

Two forces F, and F, act on a 2.20-kg object. F, = 25.0 N and F, = 12.0 N. 90.0° 60.0° 15 (a) Find the acceleration of the object for the configuration of forces shown in Figure (a). magnitude m/s2 direction ° (counterclockwise from F,) (b) Find the acceleration of the object for the configuration of forces shown in Figure (b). honagnitude m/s2 direction (counterclockwise from F,)

Two forces F, and F, act on a 2.20-kg object. F, = 25.0 N and F, = 12.0 N. 90.0° 60.0° 15 (a) Find the acceleration of the object for the configuration of forces shown in Figure (a). magnitude m/s2 direction ° (counterclockwise from F,) (b) Find the acceleration of the object for the configuration of forces shown in Figure (b). honagnitude m/s2 direction (counterclockwise from F,)

College Physics

11th Edition

ISBN:9781305952300

Author:Raymond A. Serway, Chris Vuille

Publisher:Raymond A. Serway, Chris Vuille

Chapter1: Units, Trigonometry. And Vectors

Section: Chapter Questions

Problem 1CQ: Estimate the order of magnitude of the length, in meters, of each of the following; (a) a mouse, (b)...

See similar textbooks

Similar questions

A telephone pole has three cables pulling as shown from above, with F₁ = (300.0 N, 500.0 N), F2 = (-200.0 N, 0.000 N), and F3 = (0.000 N, -800.0 N). Find the magnitude and direction of this net force. Note: The angle measured from the positive x-axis into the counter-clockwise direction is positive. 316.2 N, -71.57⁰. 316.2 N, 71.57⁰. 320.0 N, -71.57⁰. 316.2 N, -288.4⁰. 316.2 N, 18.43⁰. 316.2 N, -18.43⁰. 320 N, - O 320.0 N, -72.00⁰. -70⁰.
Please
Compute the y-component of the resultant of the concurrent forces shown in N. P1 = 299 N, P2 = 444 N, P3 = 466 N, P4 = 172 N, 0119, 02-32, and 03 - 39. Write numerical value only in 2 decimal places. P1 P4 03 0₂ 0₂₁ P3 _._ + X P2
Three vector forces with magnitudes of F₁-4.79N, F2=7.32N and F3-2.81N act on a particle of mass m = 7.73 kg as shown in Fig. Calculate the magnitude of the Net force acting on the particle. Given additional Data: 0₁-65° 03-22° Input your answer in N using 3 significant figures. F₁ 0₁ F₂ F3
Forces of 60 N at 170 degrees, and 40 N at an angle of 220 degrees, measured counter-clockwise from the positive x- axis, act on an object. What are the components (F1x, F1y) of the first force force (in Newtons)? Submit Answer Tries 0/2 What are the components (F2x, F2y) of the second force force (in Newtons)? Submit Answer Tries 0/2 What are the components (Fx, Fy) of the resultant force (in Newtons)? Submit Answer Tries 0/2 What is the magnitude of the resultant force (in Newtons)? Submit Answer Tries 0/2 What is the angle of the resultant force with respect to x-axis? (positive values only) Submit Answer Tries 0/2
A mountain climber, in the process of crossing between two cliffs by a rope, pauses to rest. She weighs 565 N. Find the tensions in the rope to the left and to the right of the mountain climber. 80.0(right side) 65.0°(left side)
Theed thẻ answer quiCkly FR is the resultant of the forces F1, F2 and F3. Find the magnitude of force F2 and the distance x. F 10N 75cm 1m Fa= 40N Fz 20N
A 3.0 kg box is pulled by applying a force with magnitude 8.0 N at an angle of 60⁰ above the horizontal as shown below, what are the x and y components of the force, F.
Please hand writing
Your friend has slipped and fallen. To help her up, you pull with a force F. The vertical component of this force is 130 N and the horizontal component is 150 N. Find the magnitude and the angle of F
The helicopter view in the figure below shows two people pulling on a stubborn mule. (Take F₁ = 127 N and F₂ = 69.0 N.) F₂ direction 75.00 60.0⁰ (a) Find the single force that is equivalent to the two forces shown. X magnitude Your response differs from the correct answer by more than 10%. Double check your calculations. N ° counterclockwise from the +x-axis (b) Find the force a third person would have to exert on the mule to make the net force equal to zero. magnitude N direction ° counterclockwise from the +x-axis
Determine the resultant ?R of the three tension forces acting on the eyt bolt. Find the magnitude of R and the angle θx which R makes with the positive x-axis. Note that F1= 563 N, F2= 345 N and F3= 296 N.