Question
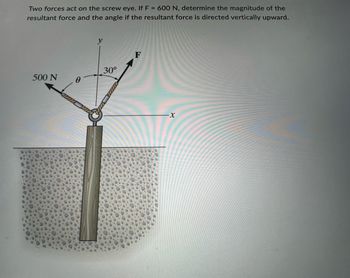
Transcribed Image Text:### Problem Statement on Equilibrium of Forces
**Topic:** Vector Addition and Resultant Force Calculation
#### Background:
Two forces act on the screw eye. The objective is to determine the magnitude of the resultant force and the angle if the resultant force is directed vertically upward.
#### Given Data:
- Force \( F \) is 600 N.
- There is an angle of 30° between force \( F \) and the vertical axis \( y \).
- Another force of 500 N is applied at an angle \( \theta \) to the horizontal axis \( x \).
#### Diagram Explained:
The image depicts a screw eye anchored to a surface with two ropes extending from the screw eye, each exerting a force.
- The first force is labeled as 500 N and is applied at an unknown angle \( \theta \) to the horizontal \( x \)-axis, directed upward and to the left.
- The second force \( F \) is 600 N and is applied at a 30° angle from the vertical \( y \)-axis, directed upward and to the right.
- The coordinate system is marked with \( x \)-axis (horizontal) and \( y \)-axis (vertical).
#### Questions to Consider:
1. **What is the magnitude of the resultant force?**
2. **What is the angle \( \theta \) at which the 500 N force is applied to ensure that the resultant force is directed vertically upward?**
#### Detailed Explanation:
To solve for these unknowns, we can use the principles of vector addition and trigonometry. This involves breaking down each force into its horizontal and vertical components, then setting up equations to ensure that the resultant force is directed vertically upwards.
#### Steps:
1. **Resolve each force into its components**:
- For the 600 N force:
- \( F_{y} = 600 \cos 30^\circ \)
- \( F_{x} = 600 \sin 30^\circ \)
- For the 500 N force:
- \( F_{x'} = 500 \cos \theta \)
- \( F_{y'} = 500 \sin \theta \)
2. **Equate the horizontal component to zero (since the resultant force is vertically upward)**:
- \( F_{x} + F_{x'} = 0 \)
This yields:
\[
600 \sin 30
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 11 images

Knowledge Booster
Similar questions
- please answer this questionarrow_forwardYou have enrolled in a scuba diving class and while swimming under water in a nearby lake you look up and note that the Sun appears to be at an angle of 17° from the vertical. At what angle above the horizon does the diving instructor standing on shore see the Sun? °arrow_forwardA drinking straw is partly immersed in some water in a glass. If the straw makes an angle of 40 degrees (40) with the water surface what angle does the submerged part of the straw appear to make with the surface? Assume you are looking vertically downwards. 24.1 degrees (24.1) 50 degrees (50"). 61.8 degrees (618) 32.2 degrees (32.2) 734 degrees (73.4) O000 Oarrow_forward
- When a young girl looks in a 6.0-cm radius, spherical Christmas tree ornament, she sees an image of her face that is upright and four times smaller than its actual size. How close is her face to the ornament? a. 9.0 cm b. 7.0 cm c. 5.0 cm d. 8.0 cm e. 6.0 cmarrow_forwardIP A magician wishes to create the illusion of a 2.66- m-tall elephant. He plans to do this by forming a virtual image of a 46.0-cm-tall model elephant with the help of a spherical mirror. You may want to review (Pages 923 - 928). If the model must be placed 2.65 m from the mirror, what radius of curvature is needed? R= -4.52 1Π ΑΣΦ 4 Submit Previous Answers Request Answer Part C * Incorrect; Try Again; 2 attempts remaining How far from the mirror will the image be formed? di 15.3 m Submit ? Previous Answers m Review ✓ Correct Here we learn how to determine the distance from the mirror to the image. The image distance is negative, thus, the image is behind the mirror.arrow_forwardCurrent Attempt in Progress The drawing shows a laser beam shining on a plane mirror that is perpendicular to the floor. The angle of incidence is 33.0°. The beam emerges from the laser at a point that is 1.10 m from the mirror and 1.80 m above the floor. After reflection, how far from the base of the mirror does the beam strike the floor? Number i eTextbook and Media Save for Later Units 1.10 m- 33.0 Floor 1.80 m Attempts: 0 of 6 used Submit Answerarrow_forward
- A man shines a flashlight from a boat into the water, illuminating a rock as in the figure below. What is the angle of incidence ₁ (in degrees)? HINT O 01 2.72 ml 1.51 m-arrow_forwardA small logo is embedded in a thick block of transparent material (n = 1.52), 2.42 cm beneath the top surface of the block. The block is put under water (n = 1.333), so there is 1.54 cm of water above the top surface of the block. The logo is viewed from directly above by an observer in air. How far beneath the top surface of the water does the logo appear to be? Number Unitsarrow_forwardQuestion in the attachmentsarrow_forward
- 34. An incident light ray enters a prism system at 0 degrees to normal. The larger prism has a mirror like surface. What angle from the normal will the light ray exit the system? A. 36.6 degreesB. 16.1 degreesC. 24.6 degreesD. 73.9 degreesarrow_forwardSolve and exarrow_forwardTwo forces act on the screw eye. If F₁ = 400 N and F₂ = 600 N, determine the angle between them, so that the resultant force has a magnitude of FR = 800 N.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios