College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Related questions
Concept explainers
Question
Two blocks are connected by a massless rope. The rope passes over an ideal (frictionless and massless) pulley such that one block with mass m1 = 13.25 kg is on a horizontal table and the other block with mass m2 = 9.5 kg hangs vertically. Both blocks experience gravity and the tension force, T. Use the coordinate system specified in the diagram.
1. Carefully consider how the accelerations a1 and a2 are related. Solve for the magnitude of the acceleration, a1, of the block of mass m1, in meters per square second.
2. Find the magnitude of the tension in the rope, T, in newtons.
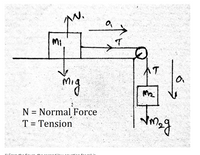
Transcribed Image Text:The image depicts a classic physics problem involving two masses connected by a string over a pulley. This setup is commonly used to study the principles of classical mechanics, specifically tension and acceleration in connected systems.
### Diagram Details:
- **Mass \( m_1 \):**
- Positioned on a horizontal surface.
- Forces acting on it:
- Downward gravitational force \( m_1g \).
- Upward normal force \( N \).
- Horizontal tension \( T \) in the string.
- Horizontal acceleration \( a \) to the right.
- **Pulley System:**
- The string passes over a pulley, which is assumed to be frictionless.
- Tension \( T \) is the same on both sides of the pulley if the string and pulley are ideal (massless and frictionless).
- **Mass \( m_2 \):**
- Suspended vertically.
- Forces acting on it:
- Downward gravitational force \( m_2g \).
- Upward tension \( T \) in the string.
- Acceleration \( a \) downward.
### Key Concepts:
- **Normal Force (N):** The perpendicular contact force exerted by a surface on an object.
- **Tension (T):** The force conducted along the string, opposing the weight on the suspended mass and pulling the mass on the surface.
This setup allows exploration of Newton’s Second Law (\( F = ma \)) as applied to different masses and helps in determining the relationship between the forces, tension, and acceleration in such systems.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 3 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- On a hot summer day, a young girl swings on a rope above the local swimming hole (Figure 1). When she lets go of the rope her initial velocity is 2.10 m/s at an angle of 35.0 ° above the horizontal. You may want to review (Pages 99 - 101). Part A If she is in flight for 0.611 S, how high above the water was she when she let go of the rope? ? h = Imarrow_forwardPlease answers parts a and barrow_forwardA baseball is hit with a speed of 30.0 m/s at an angle of 49.0 . It lands on the flat roof of a 10.0 m -tall nearby building. Part A If the ball was hit when it was 1.3 m above the ground, what horizontal distance does it travel before it lands on the building? Express your answer using two significant figures. Ax = Submit Request Answerarrow_forward
- Part A A shot-putter throws the "shot" (mass = 7.3 kg) with an initial speed of 14.1 m/s at a 43.0 ° angle to the horizontal. Calculate the horizontal distance traveled by the shot if it leaves the athlete's hand at a height of 2.15 m above the ground. Express your answer using three significant figures and include the appropriate units. HA ? d = Value Units Submit Request Answerarrow_forwardjust parts d-farrow_forwardA small ball is attached to the lower end of a 0.800-m-long string, and the other end of the string is tied to a horizontal rod. The string makes a constant angle of 41.8° with the vertical as the ball moves at a constant speed in a horizontal circle. Part A If it takes the ball 1.55 s to complete one revolution, what is the magnitude the radial acceleration of the ball? Express your answer with the appropriate units. arad = Value Units ?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press 
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON
Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON