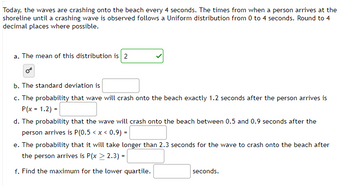
Today, the waves are crashing onto the beach every 4 seconds. The times from when a person arrives at theshoreline until a crashing wave is observed follows a Uniform distribution from 0 to 4 seconds. Round to 4decimal places where possible.a. The mean of this distribution is 2Orb. The standard deviation isc. The probability that wave will crash onto the beach exactly 1.2 seconds after the person arrives isP(x = 1.2) =d. The probability that the wave will crash onto the beach between 0.5 and 0.9 seconds after theperson arrives is P(0.5 < x < 0.9) =e. The probability that it will take longer than 2.3 seconds for the wave to crash onto the beach afterthe person arrives is P(x > 2.3) =f. Find the maximum for the lower quartile.seconds.

As per our guidelines we are suppose to answer only three subparts kindly post the remaining…

Answered: Today, the waves are crashing onto the…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Similar questions

The average number of miles driven on a full tank of gas in a certain model car before its low-fuel light comes on is 399. Assume this mileage follows the normal distribution with a standard deviation of What is the probability that, before the low-fuel light comes on, the car will travel between 328 and 348 miles on the next tank of gas? 36 miles. Complete parts a through d below. (Round to four decimal places as needed.
Assume that the readings on the thermometers are normally distributed with a mean of 0°C and a standard deviation of 1.00°C. A thermometer is randomly selected and tested. Find the probability that the reading is between 1.5°C and 1.71°C.
Today, the waves are crashing onto the beach every 5.3 seconds. The times from when a person arrives at the shoreline until a crashing wave is observed follows a Uniform distribution from 0 to 5.3 seconds. Round to 4 decimal places where possible. a. The mean of this distribution is b. The standard deviation is c. The probability that wave will crash onto the beach exactly 3.3 seconds after the person arrives is P(x = 3.3) = d. The probability that the wave will crash onto the beach between 1.9 and 2.3 seconds after the person arrives is P(1.9 3.26) = f. Find the minimum for the upper quartile. seconds.
Today, the waves are crashing onto the beach every 4.5 seconds. The times from when a person arrives at the shoreline until a crashing wave is observed follows a Uniform distribution from 0 to 4.5 seconds. Round to 4 decimal places where possible. a. The mean of this distribution is b. The standard deviation is c. The probability that wave will crash onto the beach exactly 1.7 seconds after the person arrives is P(x = 1.7) = d. The probability that the wave will crash onto the beach between 1.5 and 3.9 seconds after the person arrives is P(1.5 1) = f. Find the maximum for the lower quartile. seconds.
The IQ's in a certain population are normally distributed with a mean score of 104 and a standard deviation of 14. If we select a person at random from this population, find the probability that their IQ will be: 1. Find the 67th percentile of IQ's in this population. 2. Find the 20 The percentile of IQ's in this population 3. Find the IQR of IQ's in this population.
Today, the waves are crashing onto the beach every 5.6 seconds. The times from when a person arrives at the shoreline until a crashing wave is observed follows a Uniform distribution from 0 to 5.6 seconds. Round to 4 decimal places where possible. a. The mean of this distribution is b. The standard deviation is c. The probability that wave will crash onto the beach exactly 0.7 seconds after the person arrives is P(x = 0.7) = d. The probability that the wave will crash the beach between 1.6 and 5.1 seconds after the person arrives is P(1.6 3.72) = f. Suppose that the person has already been standing at the shoreline for 0.8 seconds without a wave crashing in. Find the probability that it will take between 1.4 and 3.3 seconds for the wave to crash onto the shoreline. g. 65% of the time a person will wait at least how long before the wave crashes in? seconds. h. Find the minimum for the upper quartile. seconds.
need help with this, need answers for A B C D E F thanks!
In a normal distribution, x = 5 and 2=-1.25. This tells you that x = standard deviations to the (right or left) of the mean.
Suppose that the speeds of cars travelling on California freeways are normally distributed with a mean of 62 miles/hour. The highway patrol's policy is to issue tickets for cars with speeds exceeding 75 miles/hour. The records show that exactly 2% of the speeds exceed this limit. Find the standard deviation of the speeds of cars travelling on California freeways. Carry your intermediate computations to at least four decimal places. Round your answer to at least one decimal place.
please answer in 30 minutes.
Today, the waves are crashing onto the beach every 4.1 seconds. The times from when a person arrives at the shoreline until a crashing wave is observed follows a Uniform distribution from 0 to 4.1 seconds. Round to 4 decimal places where possible. a. The mean of this distribution is b. The standard deviation is C. The probability that wave will crash onto the beach exactly 2.8 seconds after the person arrives is P(x = 2.8) = d. The probability that the wave will crash onto the beach between 0.4 and 1.9 seconds after the person arrives is P(0.4 0.82) = f. Suppose that the person has already been standing at the shoreline for 0.5 seconds without a wave crashing in. Find the probability that it will take between 1 and 4 seconds for the wave to crash onto the shoreline. g. 26% of the time a person will wait at least how long before the wave crashes in? seconds. h. Find the maximum for the lower quartile. seconds.
Today, the waves are crashing onto the beach every 5.4 seconds. The times from when a person arrives at the shoreline until a crashing wave is observed follows a Uniform distribution from 0 to 5.4 seconds. Round to 4 decimal places where possible. a. The mean of this distribution is 2.7 b. The standard deviation is c. The probability that wave will crash onto the beach exactly 4.1 seconds after the person arrives is P(x = 4.1) =| d. The probability that the wave will crash onto the beach between 1.8 and 4.8 seconds after the person arrives is P(1.8 2.28) = f. Find the maximum for the lower quartile. seconds.

SEE MORE QUESTIONS

Recommended textbooks for you

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

Elementary Statistics: Picturing the World (7th E…

Statistics

ISBN:

9780134683416

Author:

Ron Larson, Betsy Farber

Publisher:

PEARSON

The Basic Practice of Statistics

Statistics

ISBN:

9781319042578

Author:

David S. Moore, William I. Notz, Michael A. Fligner

Publisher:

W. H. Freeman

Introduction to the Practice of Statistics

Statistics

ISBN:

9781319013387

Author:

David S. Moore, George P. McCabe, Bruce A. Craig

Publisher:

W. H. Freeman

SEE MORE TEXTBOOKS