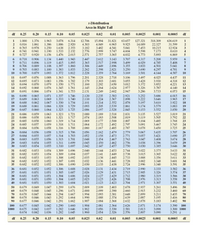
Question 4 This table represents the t-Distribution with the area in the right tail for various degrees of freedom (df) and probability levels. The table is organized with degrees of freedom (df) listed both in the leftmost column and the rightmost column, while the top row shows different probability levels ranging from 0.25 to 0.0005.### Table Breakdown:- **Columns:** - The first column and the last column list degrees of freedom (df) from 1 to 1000. - The columns between them represent probability levels: 0.25, 0.20, 0.15, 0.10, 0.05, 0.025, 0.02, 0.01, 0.005, 0.0025, 0.001, and 0.0005.- **Rows:** - Each row corresponds to a specific value of degrees of freedom. - Each cell within the table presents the critical value of t for the corresponding probability level and degrees of freedom.### How to Use the Table:1. **Identify the Degrees of Freedom (df):** Locate the appropriate row for the degrees of freedom you need.2. **Select the Probability Level:** Choose the column for the probability level corresponding to your desired tail area.3. **Find the Critical t-Value:** The intersection of the chosen row and column provides the critical t-value.### Example:- For **df = 10** and a **probability level of 0.05**, the critical t-value is **1.812**. This means that for 10 degrees of freedom, the cutoff for the right tail of the t-distribution is 1.812 for a 0.05 level of significance.This table is commonly used in statistical analyses, such as hypothesis testing, where critical values are required to make decisions based on t-distributions. It assists in determining whether to reject a null hypothesis by comparing the calculated test statistic to the critical t-value obtained from the table. To test \( H_0: \mu = 40 \) versus \( H_1: \mu < 40 \), a random sample of size \( n = 25 \) is obtained from a population that is known to be normally distributed. Complete parts (a) through (d) below.(a) If \( \bar{x} = 37.4 \) and \( s = 13.6 \), compute the test statistic.\[ t_0 = -0.956 \] (Round to three decimal places as needed.)(b) If the researcher decides to test this hypothesis at the \( \alpha = 0.05 \) level of significance, determine the critical value(s). Although technology or a t-distribution table can be used to find the critical value, in this problem use the t-distribution table given.Critical Value: \(-1.711\) (Round to three decimal places. Use a comma to separate answers as needed.)(c) Draw a t-distribution that depicts the critical region. Choose the correct answer below.Option A: A t-distribution curve with the left tail shaded indicates the critical region on the left side.Option B: A t-distribution curve with a central peak and the left tail shaded, indicating one-tailed test critical region.Option C: A t-distribution curve with both tails shaded indicating a two-tailed test, with critical regions on both ends.(d) Choose the correct critical region illustration:- (A) is likely the correct depiction if testing for a mean less than a certain value, signifying a left-tailed test.

To test Ho: H= 40 versus H,: u< 40, a random sample of size n=25 is obtained from a population that is known to be normally distributed. Complete parts (a) through (d) below. E Click here to view the t-Distribution Area in Right Tail. (a) If x = 37.4 and s= 13.6, compute the test statistic. to = - 0.956 (Round to three decimal places as needed.) (b) If the researcher decides to test this hypothesis at the a = 0.05 level given. significance, determine the critical value(s). Although technology or a t-distribution table can be used to find the critical value, in this problem use the t-distributic Critical Value: - 1.711 (Round to three decimal places. Use a comma to separate answers as needed.) (c) Draw a t-distribution that depicts the critical region. Choose the correct answer below. O A. OB. Oc. Q -/2 0 /2