
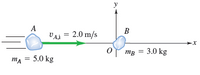
This is a two-dimensional version of a conservation-of-momentum problem. Now we will have to keep track of both the x and y components of the momentum of each object in the system. (Figure 1) shows two chunks of ice sliding on the surface of a frictionless frozen pond. Chunk A, with mass mA=5.0kg, moves with initial velocity vA,i=2.0m/s parallel to the x axis. It collides with chunk B, which has mass mB=3.0kg and is initially at rest. After the collision, the velocity of A is found to be vA,f=1.0m/s in a direction at an angle α=30∘ with the initial direction (Figure 2). What is the final velocity of B (magnitude and direction)?
PART A. b)If chunk B has an initial velocity of magnitude 1.6 m/s in the +y direction instead of being initially at rest, find the final magnitude of its velocity.
c)Using Part A, find the final direction of the velocity.
Trending nowThis is a popular solution!
Step by stepSolved in 7 steps with 1 images

- Two objects had a direct collision. Initially, object A is travelling as fast as object B but in the opposite direction. During collision the momentums are conserved. How much faster is A compared to B after collision, if B weighs 3 times as much as A and is travelling now at half the its initial speed? O 5 times O 6 times O 4 times O 3 timesarrow_forwardA woman of mass m = 63 kg runs at a velocity vi = 1.53 m/s before jumping on a skateboard that is initially at rest. After jumping on the board the woman has a velocity vf = 1.42 m/s.b. What is the mass of the skateboard in kilograms? mb =c. The woman soon loses his balance and falls backwards off the board at a velocity of 1.0 m/s. Assuming momentum is conserved in this process, what is the skateboard's new velocity in meters per second? [Note: this may not be a very good assumption, as there can be significant friction in the ball bearings of the skateboard]arrow_forwardPing and Leni of equal mass collide on a horizontal frictionless surface. Before the collision, Ping P is at rest while Leni L has a constant velocity of 12 m/s. After the collision, they are stuck together. What is the speed of the composite body (P + L) after the collision? (A) 3 m/s В 6 m/s C) 9 m/s 12 m/sarrow_forward
- Two 465g blocks of wood are 2 m apart on a frictionless table. A 15g bullet is fired at 419 m/s toward the blocks. it passes all the way through the first block then embeds itself in the second block. The speed of the first book in merely afterwards is 7 m/s. What is the speed of the second block after the bullet stops in it? Answer to 3 sig figs.arrow_forwardBetty (mass 35 kg) stands on an ice rink as Bubbles (her hyperactive puppy, mass 8.6 kg)) runs towards her and leaps into her arms. If they move off together with a speed of 0.76 m/s, how fast (in m/s) was Bubbles moving when Betty caught her?arrow_forwardA 0.2 kg rubber ball is dropped from the window of a building. It strikes the sidewalk below at 30 m/s and rebounds at 20 m/s. The magnitude of the change in momentum of the ball as a result of the collision with the sidewalk is _______.arrow_forward
- What is the numeric answer to problem #24 on page 293? This is a fairly challenging problem.Just remember that Momentum is conserved __________________arrow_forwardIt is generally a good idea to gain an understanding of the size of units. Consider each object and calculate the magnitude of their momentum in SI units. A ladybug with mass 28.50 milligrams flies by your head at 3.75 km/h. magnitude of the momentum: kg-m/s A 37.90 km boy walks at 4.05 km/h. magnitude of the momentum: kg-m/s A car with mass 841 kg is moving at a speed of 41.3 km/h. magnitude of the momentum: kg-m/sarrow_forwardThe carbon isotope 14C is used for carbon dating of archaeological artefacts. 14C decays to 14N by a process known as beta decay, in which the nucleus emits an electron (also known as a beta particle) and a subatomic particle called a neutrino. In one such decay, the electron and the neutrino are emitted in opposite directions to each other. The electron has a speed of 5 x 10 m/s and the neutrino has a momentum of 5 x 1024 kg m/s. n as What is the recoil speed of the resulting 14N nucleus? (Take the mass of the carbon-14 and nitrogen-14 nuclei to be 2.34 x 10 26 kg and the mass of the electron to be 9.11 x 1031 kg. If you were aware of such things and concerned, please ignore relativistic effects.)arrow_forward
- Need help with this physics question !arrow_forwardThe carbon isotope 14C is used for carbon dating of archaeological artefacts. 14C decays to 14N by a process known as beta decay, in which the nucleus emits an electron (also known as a beta particle) and a subatomic particle called a neutrino. In one such decay, the electron and the neutrino are emitted in opposite directions to each other. The electron has a speed of 4 x 107 m/s and the neutrino has a momentum of 8 × 10-24 kg m/s. What is the recoil speed (in m/s) of the resulting 14N nucleus? (Take the mass of the carbon-14 and nitrogen-14 nuclei to be 2.34 x 10-26 kg and the mass of the electron to be 9.11 x 1031 kg. If you were aware of such things and concerned, please ignore relativistic effects.)arrow_forwardYou drop a 0.15-kg ball to the floor from a height of 2.7 m, and it bounces to a height of 1.2 m. What is the magnitude of the change in its momentum as a result of the bounce? Express your answer with the appropriate units. |Δpy| =arrow_forward
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON





