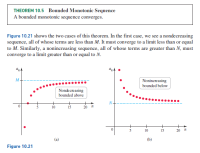
THEOREM 10.5 Bounded Monotonic Sequence A bounded monotonic sequence converges. Figure 10.21 shows the two cases of this theorem. In the first case, we see a nondecreasing sequence, all of whose terms are less than M. It must converge to a limit less than or equal to M. Similarly, a nonincreasing sequence, all of whose terms are greater than N, must converge to a limit greater than or equal to N. M Nonincreasing bounded below Nondecreasing bounded above 15 20 10 15 20 n (a) (b) Figure 10.21

Show that the infinite sequence 5. an = √ (n2 + 1) − √ (n2 − 1) (n ≥ 1) converges by showing that it is monotone and bounded. You do not need to find the limit of the sequence

Suppose we have a recursive sequence ƒ1, ƒ2, ƒ3, . . .. For the purposes of this problem, it does not matter exactly how the fi are defined, only that they are recursively defined. = i=1 For integer n ≥ 1, let P(n) be the predicate that Σï-1 fi = 2fn+2 − 3. Don't worry about whether this predicate "makes sense"; we haven't defined the fi so you won't be able to "make sense" of the P(n). It's not important for this problem. Consider a proof by induction that Vn ≥ 1: P(n). Suppose we've gotten to the inductive step, and suppose that the first steps of the inductive step are k+1 k+1 Σ1 fi = f1 + f2 + Σh fi = f₁ + f2 + Σkt k+1, i=3 (fi−1 + fi−2) = f₁ + f2 + ¹ fi- 1 + k fi 2 f1 k+1 k+1 k = f1 + f2 + Σh_2 fi + [h=1² fi i=2 = f2 + Σ²²₁ fi+fi i=1 i=1 True or false: Based on the information given, we will need strong induction for this proof. True False