
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
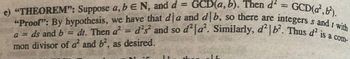
Transcribed Image Text:**Theorem**: Suppose \( a, b \in \mathbb{N} \), and \( d = \text{GCD}(a, b) \). Then \( d^2 = \text{GCD}(a^2, b^2) \).
**Proof**: By hypothesis, we have that \( d \mid a \) and \( d \mid b \), so there are integers \( s \) and \( t \) with \( a = ds \) and \( b = dt \). Then \( a^2 = d^2s^2 \) and so \( d^2 \mid a^2 \). Similarly, \( d^2 \mid b^2 \). Thus \( d^2 \) is a common divisor of \( a^2 \) and \( b^2 \), as desired.

Transcribed Image Text:**Proof Evaluation**
(This type of exercise will appear occasionally): Each of the following is a proposed "proof" of a "theorem". However, the "theorem" may not be a true statement, and even if it is, the "proof" may not really be a proof. You should read each "theorem" and "proof" carefully and decide and state whether or not the "theorem" is true. Then:
- If the "theorem" is false, find where the "proof" fails. (There has to be some error.)
- If the "theorem" is true, decide and state whether or not the "proof" is correct. If it is not correct, find where the "proof" fails.
Expert Solution
arrow_forward
Step 1
We modify the missing arguments in the proof and explain in detail below.
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
- If m is a positive integer, then show that xl-c (1-x) r(c + m) 2F1 (-m, a + m; c; x ) = oved -r (c) dm [x²+m-1 (1-x)²-c+m] r(c)arrow_forwardLet a-2i+ 3jk, b=4i+) and c=1+3)+2k. If d is such that da-9db-7 and d c-6, then d is equal to 01-3j-2k 01-3j+ 2k 04+31-2k Oi-3) 2karrow_forwardl, tet and m be integed, prove that +5 19 17/27+3m iff, 17/9narrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

