
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Please help me answer my homework.
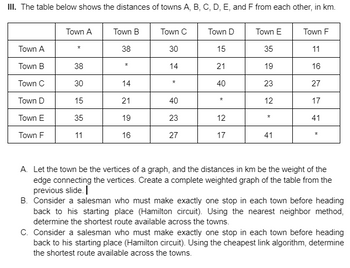
Transcribed Image Text:III. The table below shows the distances of towns A, B, C, D, E, and F from each other, in km.
Town A
Town B
Town C
Town D
Town E
Town F
Town A
*
38
30
15
35
11
Town B
38
*
14
21
19
16
Town C
30
14
*
40
23
27
Town D
15
21
40
*
12
17
Town E
35
19
23
12
*
41
Town F
11
16
27
17
41
*
A. Let the town be the vertices of a graph, and the distances in km be the weight of the
edge connecting the vertices. Create a complete weighted graph of the table from the
previous slide.
B. Consider a salesman who must make exactly one stop in each town before heading
back to his starting place (Hamilton circuit). Using the nearest neighbor method,
determine the shortest route available across the towns.
C. Consider a salesman who must make exactly one stop in each town before heading
back to his starting place (Hamilton circuit). Using the cheapest link algorithm, determine
the shortest route available across the towns.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 6 steps with 2 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Can you answer letter C please.
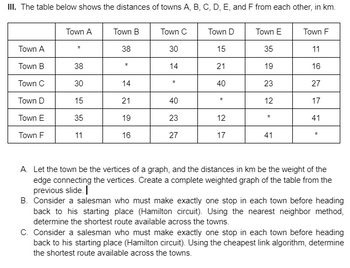
Transcribed Image Text:III. The table below shows the distances of towns A, B, C, D, E, and F from each other, in km.
Town A
Town B
Town C
Town D
Town E
Town F
Town A
*
38
30
15
35
11
Town B
38
*
14
21
19
16
Town C
30
14
*
40
23
27
Town D
15
21
40
*
12
17
Town E
35
19
23
12
*
41
Town F
11
16
27
17
41
*
A. Let the town be the vertices of a graph, and the distances in km be the weight of the
edge connecting the vertices. Create a complete weighted graph of the table from the
previous slide.
B. Consider a salesman who must make exactly one stop in each town before heading
back to his starting place (Hamilton circuit). Using the nearest neighbor method,
determine the shortest route available across the towns.
C. Consider a salesman who must make exactly one stop in each town before heading
back to his starting place (Hamilton circuit). Using the cheapest link algorithm, determine
the shortest route available across the towns.
Solution
by Bartleby Expert
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Can you answer letter C please.

Transcribed Image Text:III. The table below shows the distances of towns A, B, C, D, E, and F from each other, in km.
Town A
Town B
Town C
Town D
Town E
Town F
Town A
*
38
30
15
35
11
Town B
38
*
14
21
19
16
Town C
30
14
*
40
23
27
Town D
15
21
40
*
12
17
Town E
35
19
23
12
*
41
Town F
11
16
27
17
41
*
A. Let the town be the vertices of a graph, and the distances in km be the weight of the
edge connecting the vertices. Create a complete weighted graph of the table from the
previous slide.
B. Consider a salesman who must make exactly one stop in each town before heading
back to his starting place (Hamilton circuit). Using the nearest neighbor method,
determine the shortest route available across the towns.
C. Consider a salesman who must make exactly one stop in each town before heading
back to his starting place (Hamilton circuit). Using the cheapest link algorithm, determine
the shortest route available across the towns.
Solution
by Bartleby Expert
Knowledge Booster
Similar questions
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

