The subscript s indicates that s is being held constant. Then dividing by dt, we have du/dt as before. We could also use derivatives instead of differentials. By an equation like (5.1), we have du dz əz ət ди ди дх ди ду (7.2) Əx dt dy dt where we have written all thet derivatives as partials since u, x, y, and z depend on both s and t. Using (7.2), we get du = (2x + 2y)(2t)+ (2x – In z)(-2t) + (-2) (2) = 4yt + 2t ln z – 2y It is sometimes useful to write chain rule formulas in matrix form (for matrix multiplication, see Chapter 3, Section 6). Given, as above, u = f(x,y, z), x(s, t), y(s, t), z(s,t), we can write equations like (7.2) in the following matrix form: as ди ди ds dt ди ди ди dx dy dz, ду ду (7.3) ds dz dz ds dt Sometimes (7.3) is written in the abbreviated form d(u) a(s,t) a(u) a(x, y, z) d(x, y, z) d(s,t) which is reminiscent of dy dy dx %3D dt dx dt but be careful of this for two reasons: (a) It may be helpful in remembering the formula but to use it you must understand that it means the matrix product (7.3). (b) The symbol d(u, v)/a(x, y) usually means a determinant rather than a matrix of partial derivatives see Chapter 5, Section 4]. Again in these problems, you may say, why not just substitute? Look at the following problem. 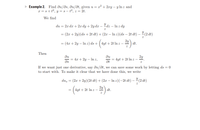Example 2. Find du/ðs, du/dt, given u = x² + 2xy – y ln z and x = s+t2, y= s – t2, z = 2t. We find du = 2x dx + 2x dy + 2y dx – 2dz – In z dy = (2x + 2y)(ds + 2t dt) + (2x – In 2)(ds – 2t dt) – 2 (2 dt) 2y = (4x + 2y – In z) ds + ( 4yt + 2t ln z – dt. Then ди = 4x + 2y – In z, ди = 4yt + 2t I z 2y Əs If we want just one derivative, say du/at, we can save some work by letting ds = 0 to start with. To make it clear that we have done this, we write (2 dt) du, = (2x + 2y)(2t dt) + (2x – In z)(-2t dt) – 2y 4yt + 2t ln z dt.

If+y = 25 and dz/dt = 5, find dy/dt when y is positive and %3D %3D (a) z = 0 dy/dt = 0 (b) z = 1 = P/hp (C) z=3 dy/dt =