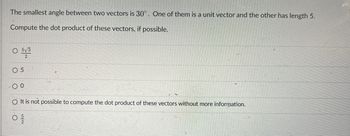
The smallest angle between two vectors is 30°. One of them is a unit vector and the other has length 5. Compute the dot product of these vectors, if possible. O 5√3 2 O 5 00 O It is not possible to compute the dot product of these vectors without more information. 01/10 O

Q: 1 2 3 - + 1 4 = 3 ₂ 3 + ₁ = 1 ₁x₂2x3 + 2x4 = 0

A:

Q: Find an equation for the surface that contains all such points P that has Problem 2. equal distance…

A: Distance is defined as the algebraic expression that gives the distance between the pair of points…

Q: The quantity demanded of a hand-woven rug is 3000 per month, when the unit price is $500. For each…

A:

Q: Tax, ox], is either empty, a single point, or a bounded closed interval. ΧΕΙ Exercise 2.1.7 a. Show…

A:

Q: E.y=600- 10" 4. The half-life of nickel-63 is 100 years. A students says, "An artifact with…

A: From nature decay law we have                                    x = c e-k t  ------------- (1 )…

Q: In how many months will mony become three times itself at 9% compounded semi-annually.

A: In how many months will mony become three times itself at 9% compounded semi-annually.

Q: 0.0062 0.0025 0.0012 Let D = 0.0025 0.0049 0.0025 be a flexibility matrix, with flexibility measured…

A:

Q: Determine the set of points at which the function is continuous. x²y³ f(x, y) = 2x² + y² 1 if if…

A:

Q: C. It does not rain and I don't take an umbrella. D. It does not rain or I do not take an umbrella.…

A:

Q: Given a point P=(a, b), how would I derive a formula of 2P for the elliptic curve y^2=x^3+ax+b?

A: As per the question we have to derive and explain the formula for the addition of same point on an…

Q: Linearize f(x) = √2-x for a = 1 and use it to approximate the value of √1.5. L(x) = The approximated…

A: The given problem is to linearize the f(x) for a=1 and also to find the approximate value of √1.5…

Q: Let z = 2e i Which of the following is the conjugate z of z? O-√2+i√2 0-√2-i√2 O√2-i√2 O√2+i√2 O…

A:

Q: Are the following implications correct? If yes, prove it. Otherwise, find counterexample. (a) (A⇒C)…

A: (a) We see when A => C is False, then         (A => C) => (A ∨ C => B ∨ C) evaluates to…

Q: Find the scalar and vector projections of b onto a. a = (4, -3), b = (4,0) comp b= proj₂b =

A:

Q: For what value(s) of a and b is the function f(x) given below continuous at 0? sin (3x) f(x) = I a…

A:

Q: Exercise 1.4.6 a. Show that every closed interval [a, b] is the intersection of countably many open…

A: Exercise 1.4.6 (a) To Show: Every closed interval a, b is the intersection of countable many open…

Q: Pls do fast within 5 minutes and i will give like for sure Solution must be in typed form consider…

A: Given that f and g are differentiable functions with hx=fgx. The slope of the tangent line to the…

Q: Find an equation for the surface that contains all such points that has equal distance to the point…

A: This problem is from analytical geometry. To solve this problem I have used distance formulas.

Q: 2. Find the unique solution for the following IVP with the initial conditions stated below: x' =…

A:

Q: 4. Seven red blocks and two blue blocks are arranged in a line in a uniform rando manner. What is…

A:

Q: -[-2] - [ a. Find A and use it solve the four equations Ax=b₁, Ax=b₂ Ax=b₂, and Ax=b4 b. The four…

A: The given matrix and the vectors, A=12818, b1=-4-28, b2=1-2, b3=-2-22, and b4=0-12 We have to find…

Q: 6. (3 s) Suppose a cylindrical container containing a fluid has a drain on its side. Torricelli's…

A:

Q: P2 Consider the scalar ODE y' = K, where K is a real constant, on the interval [to, T] with initial…

A: The answer provided below has been developed in a clear step by step manner.

Q: 13. 0.) Compute limit fix, if it exists, for the following f: IR→IR ₁ × → 1×1₁ X ₁ = 1 x cases!

A:

Q: Solve the Diophantine equation 98r - 21y = 35.

A: Given: 98x-21y=35. We have to solve the Diophantine equation.

Q: let F: RR be a linear transformation, which of the following applies? A) F has to be injective B) F…

A: This problem is from linear algebra. To solve this problem we will use rank nullity theorem.

Q: Write the augmented matrix corresponding to the given system of equations: (Note: The dotted…

A: The given system of equations, 7x-z=-1010x+6y=-87y+9z=1 We have to write the augmented matrix of the…

Q: Determine whether each statement is true or false. If a statement is true, give a reason or cite an…

A: The given statements are, a) The dot product is the only inner product that can be defined in ℝn. b)…

Q: Find the matrix A of the linear transformation from R² to R³ given by 1 0 -8 x2. -4 x1 + 2 -6 T…

A:

Q: how many ways can a teacher give five different prizes to five of her 26 students?

A: I have written the answer with in the solution.  Please go through that.

Q: 2. The mean and variance of a binomial distribution are 3 and 1.2 respectively. Find n, p, and P(X <…

A: Given that The Mean of the Binomial distribution is 3 np=3 Variance is 1.2 npq=1.2 3*q=1.2 q=0.4…

Q: Solve this differential equation: dy = dt y(0) = 2 y(t) = 0.08y(1000-y)

A:

Q: Question 13. Practice If assume that r(t) is differentiable, find the derivative of the following: d…

A:

Q: What variable do you eliminate, and what do you multiply the equation (s) by? 5x + y = 9 10x - 7y =…

A:

Q: Exercise 1: Mixed quantifiers Let f(x) = 1. Prove that the limit of f in 0 does not exist, i.e. that…

A:

Q: Maria needed 8 gallons of gas to fill her car's gas tank. The mileage odometer read 36,900 miles.…

A: At the start of the trip, her car needed 8 gallons to be filled. After riding (37098-36900)miles =…

Q: Solve the following complex number problems. Solutions for complex number transformation are…

A: As you have asked to solve part A only, we're solving the same.

Q: 12. sin-t dt. Use an explicit u-substitution.

A: Given: Integral, ∫sin-1t1-t2 dtTo find: The value of given integral using an explicit…

Q: a) Compute limits. f(x), if it exists, for the follow Cases f³R DR₁ X 1X1₁ X6 ³1 Xo =1 b.) f: R^ →…

A:

Q: 7) State the maximum and minimum values if they exist. P = 2x + 7y [4x-2y ≤8 {x≥1 [0sy 4

A: Given information P=2x+7y subject to,  4x-2y≤8          x≥1   0≤y≤4.

Q: 5) Find the numbers at which fis discontinuous. At which of these numbers is f continuous from the…

A:

Q: 3. Evaluate the following integrals. dr (a) x(x - 1)³ (b) (x-1)(x² +1) dx - 4x + 5 sec²0 de tan²0 -…

A:

Q: 5. In any metric space (M, D), prove that D(a1, an) ≤ D(a₁, a2) + D(a2, a3) + + D(an-1, an), for a1,…

A: Given M,D is a metric space.   The triangle inequality holds in a metric space, which means for…

Q: Find the set of points where the complex function is analytic and get its derivativ 3z - 1 3-Z f(z):…

A: We have to find the set of all points where given function is analytic.

Q: The table below shows the production costs K(x) in dollars per month for some different production…

A: Given a table of production costs K(x) in dollars per month for production quantities x of an item.…

Q: 1. Determine whether the given series is convergent or divergent. If it is, find its sum. Σ1 (14)

A: Answer 1

Q: PS2.5 Use the definition of Ax to write the matrix equation as a vector equation, or vice versa. (a)…

A: If we have matrix form as  Ax = b Where A is m×n matrix with n columns as C1 C2 ... Cn  x is n×1…

Q: Let T: R³ → R² be a linear transformation. If u and v are vectors in R² such that T(u) [3], and T(v)…

A:

Q: i) Let {an} be a sequence satisfying an> 5 for n >> 1. If {an} converges to L, then L> 5. j) Suppose…

A: We have to check if the given statements are true or false.

Q: Write the domain in interval notation. 3) y (t)=√√√8-t 4) f(x)= x-4 x-5

A: Use the given information.