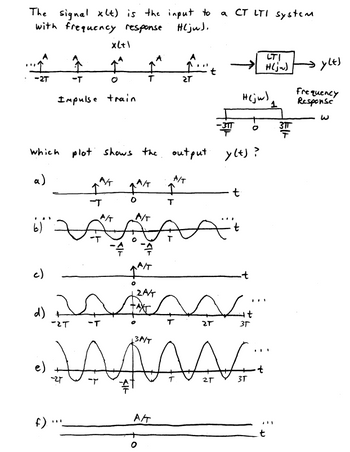
The image presents a signal processing problem involving a continuous-time (CT) linear time-invariant (LTI) system. The problem involves determining which plot correctly represents the output signal \( y(t) \).### Description:1. **Input Signal \( x(t) \):** - The input is depicted as an impulse train with impulses located at \(-2T, -T, 0, T, 2T, \ldots\). - Each impulse has an amplitude of \( A \).2. **System Characteristics:** - The system is described as a CT LTI system with a frequency response \( H(j\omega) \). - The frequency response is a rectangular function centered around zero frequency, spanning from \(-\frac{3\pi}{T}\) to \(\frac{3\pi}{T}\).3. **Diagram:** - **Block Diagram:** Shows \( x(t) \) as input to the LTI system with the output as \( y(t) \).### Task:- Determine which plot (a) to (f) represents the output \( y(t) \).### Plots:- **a)** An impulse train with impulses at \(-T, 0, T, \ldots\) and amplitude \(\frac{A}{T}\).- **b)** A continuous waveform oscillating sinusoidally between \(-\frac{A}{T}\) and \(\frac{A}{T}\), zero at intervals of \(T\). - **c)** An impulse train similar to (a) but starting from \(0\).- **d)** A sinusoidal waveform with higher frequency and amplitude spikes at integer multiples of \(T\).- **e)** Another sinusoidal waveform, oscillating between \(-\frac{A}{T}\) and \(\frac{A}{T}\), showing three cycles over one interval.- **f)** A constant line at amplitude \(\frac{A}{T}\).### Graphical Explanation:- The frequency response \( H(j\omega) \) indicates that the system acts as a low-pass filter, allowing frequencies contained within the range of \(-\frac{3\pi}{T}\) to \(\frac{3\pi}{T}\).- The choice of the correct output plot \( y(t) \) will depend on the filtering effect on the spectral components of \( x

Given: For an LTI system, x(t)=∑n=-∞∞δ(t-nT),H(jw)=1 ;-3πT≤w≤3πT0 ;Otherwise, To find: Output y(t)…

The signal xlt) is the input to a CT LTI system with frequency response H(ju). -...^^ -27 6)**: c) d) e) which plot shows the output y(t)? a) f) -T Impulse train Z x(+1 -27 -27 T A/T T A/T A/T 3A/T 2T A/T A/T ↑ T 2A/T ww TAXE H(jw) 2T -t 31 LTI H(jw) ylt) V 2T 3T t 3TT Frequency Response W

The signal xlt) is the input to a CT LTI system with frequency response H(ju). -...^^ -27 6)**: c) d) e) which plot shows the output y(t)? a) f) -T Impulse train Z x(+1 -27 -27 T A/T T A/T A/T 3A/T 2T A/T A/T ↑ T 2A/T ww TAXE H(jw) 2T -t 31 LTI H(jw) ylt) V 2T 3T t 3TT Frequency Response W

Introductory Circuit Analysis (13th Edition)

13th Edition

ISBN:9780133923605

Author:Robert L. Boylestad

Publisher:Robert L. Boylestad

Chapter1: Introduction

Section: Chapter Questions

Problem 1P: Visit your local library (at school or home) and describe the extent to which it provides literature...

See similar textbooks

Similar questions

An FM signal has a deviation of 3 kHz and a modulating frequency of 1 kHz. Its total power is 5 W, developed across a 50 Q resistive load. The carrier frelquency is 160 MHz. Based on the Bessel Table of functions, how many pairs of significant sidebands are there? A b ho hi ha ho he his he ho ha ho bo 100 0.25 0.98 0.12 0.5 0.94 024 0.03 0.75 O86 0.35 007 001 0.77 0.44 0.11 0.02 1.25 0.65 0.51 0.17 0.04 0.01 1.S 051 0.56 0.23 0.06 0.01 1.75 037 0.ss 0.29 009 0.02 022 0.58 0.35 0.13 003 0.01 225 0.08 0.55 0.40 0.17 0.05 0.01 24 0.00 0.52 0.43 0.20 006 0.02 25 00s a.so 0.45 022 007 o.02 2.75 0.16 0.43 0.47 0.26 0.10 0.03 0.01 -0.26 0.34 0.49 031 0.13 0.04 0.01 35 038 0.40 -0.07 0.36 0.43 028 0.13 0.0s 0.01 45 032 -0.23 0.22 042 0.15 0.20 0.O8 0.03 0.01 0.14 0.46 0.39 0.20 0s 0.03 0.01 -0.18 0.33 0.05 036 0.39 0.26 0.13 0.OS 0.02 0.01 5.5 0.00 -0.34 -0.12 0.26 0.40 0.32 0.19 0.09 0.03 0.01 0.15 0.28 -0.24 0.11 0.36 0.36 0.25 0.13 0.06 0.02 001 6.5 0.26 -0.15 -0.31 -0.03 028 0.37 0.30 0.18…
Question 777 Full explain this question very fast solution sent me
Ex Assuming rct= oilt and it is desired that ess Koroos, find the range of values of K for error to be within specified limit for given system. soll Ris K 915 k S(5+1) Gesiz Histal S(5+1)
I really need help solving this question, please be precise. Will rate. Question: A random variable X has the follwoing PDF: * See image What is the probability that X > 1?
Soru 30 By what factor the SNR changes if we coherently integrate 10 pulses instead of using a single pulse? A. 100 B. 1000 C. 1 D. 10000 E 10
16. Aresistor of 5.0 © an inductor of 22.0 jiH and a capacitor of 150 pF are in parallel. The frequency is 1.00 MHz. What is the complex impedance, R+ jX? = A510-/49, * B.510+/49. - C.462-ji40. = D.462+/149.
Q15. Find IBQ, Ico, VCEQ, VB, Vc, VBc for the following circuit: Jooke ITVCE B=Y0
0.5 -6 -2 4. 6. time in seconds What, signal is plotted above? O Type here to search %23 76°F A OE O 0 deete home backspack 80 QWE R
Plz solve within 30min min I vill be very thankful if u solve it and I vill upvote and vill give positive feedback But it should so quick Handwritten will be appreciated as it takes less time to solve it compared to typed
From (d) to (h) please
Digital signal processing
Cansider the systam shown below. dblase The closed Loop ranskr funchion CG/RS) ->