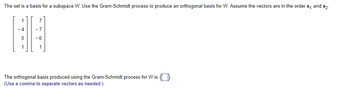
Thhis is not an assignment this is practice questions The set is a basis for a subspace W. Use the Gram-Schmidt process to produce an orthogonal basis for W. Assume the vectors are in the order x₁ and x2-17-7HH1The orthogonal basis produced using the Gram-Schmidt process for Wis(Use a comma to separate vectors as needed.)

Answered: Image /qna-images/answer/9b32733e-3306-4b37-bfd6-70f60dba6e52.jpg

Answered: The set is a basis for a subspace W.…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Similar questions

Apply table to question. Thanks!
which of the following variables is not discrete? (multiple choice) a the number of words on an 8.5x11 inch sheet of paper b the number in a group of 20 people who have college degrees c the number of attempts needed in order to successfully complete d the distance traveled by motorcycle on one gallon of gas\ f the number of countries in which a college student is enrolled
You will simulate shooting basketball free throws. Using any coin, let heads represent the ball going into the basket and tales represent the ball missing the basket. Each toss of the coin represents a shot at the free throw line. Simulate shooting 35 free throws. Make a chart on your paper similar to the one below to record your results. For each trial (toss), place an x in the appropriate column. Toss number 1 2 Went in (Heads) X Questions: 1. How many free throws went into the basket? 2. How many free throws missed the basket? Missed (Tails) X 3. What is the experimental probability that you will make the next free throw? 4. What is the experimental probability that you will miss the next free throw? 5. This simulation assumes that you have an equal chance of making the free throw or missing the free throw. Is this a correct assumption? Why? 6. How would you change this simulation to better predict a person's abilities at making free throws?
answer choices on the second screenshot
didnt answer the last question what is the value of c
which exactly are the answers?
Find the value of X.
The value of y is between negative three and positive eight inclusive. Which of the following represents y?
are you sure?

Recommended textbooks for you

Advanced Engineering Mathematics

Advanced Math

ISBN:

9780470458365

Author:

Erwin Kreyszig

Publisher:

Wiley, John & Sons, Incorporated

Numerical Methods for Engineers

Advanced Math

ISBN:

9780073397924

Author:

Steven C. Chapra Dr., Raymond P. Canale

Publisher:

McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…

Advanced Math

ISBN:

9781118141809

Author:

Nathan Klingbeil

Publisher:

WILEY

Advanced Engineering Mathematics

Advanced Math

ISBN:

9780470458365

Author:

Erwin Kreyszig

Publisher:

Wiley, John & Sons, Incorporated

Numerical Methods for Engineers

Advanced Math

ISBN:

9780073397924

Author:

Steven C. Chapra Dr., Raymond P. Canale

Publisher:

McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…

Advanced Math

ISBN:

9781118141809

Author:

Nathan Klingbeil

Publisher:

WILEY

Mathematics For Machine Technology

Advanced Math

ISBN:

9781337798310

Author:

Peterson, John.

Publisher:

Cengage Learning,

Basic Technical Mathematics

Advanced Math

ISBN:

9780134437705

Author:

Washington

Publisher:

PEARSON

Topology

Advanced Math

ISBN:

9780134689517

Author:

Munkres, James R.

Publisher:

Pearson,

SEE MORE TEXTBOOKS

The set is a basis for a subspace W. Use the Gram-Schmidt process to produce an orthogonal basis for W. Assume the vectors are in the order x₁ and x2- 1 7 -7 HH 1 The orthogonal basis produced using the Gram-Schmidt process for Wis (Use a comma to separate vectors as needed.)