For B wouldn't insertion of a value between 20 and 23 also cause a right left imbalance?
Also can you please draw what the rotations for the tree would look like as you described after inserting 18.
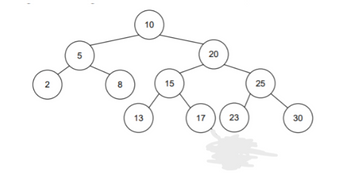
Key characteristics of an AVL tree include:
Binary Search Tree (BST) Property: Like all binary search trees, an AVL tree maintains the properties of a BST. Each node in the tree has a value, and the left subtree of a node contains values less than the node's value, while the right subtree contains values greater than the node's value.
Balancing Criterion: The balance factor for each node is defined as the height of its left subtree minus the height of its right subtree. The balance factor can be in the range of -1, 0, or 1 for all nodes in the tree. If this balance factor goes beyond this range for any node, the tree is rebalanced.
Balancing Operations: When an insertion or deletion operation disrupts the balance property of the AVL tree, one or more rotations are performed to restore balance. These rotations are designed to ensure that the balance factor for each node falls within the acceptable range.
Self-Balancing: AVL trees automatically adjust their structure during insertions and deletions, maintaining their balanced property, which distinguishes them from simple binary search trees.
Step by stepSolved in 3 steps with 4 images

- r. Is it possible to write a nonrecursive version of keys() that uses spaceproportional to the tree height (independent of the number of keys in the range)?arrow_forwardCan anyone help me with this question? Thankyou! I’ll be sure to leave a thumbs up!arrow_forwardPlease look at image and show the answer on paper the right result!arrow_forward
- Note, you are given the tree T and the edge e = (y, z) whose weight is changed; you are told its old weight w(e) and its new weight w~(e) (which you type in latex by widetilde{w}(e) surrounded by double dollar signs). In each case specify if the tree might change. And if it might change then give an algorithm to find the weight of the possibly new MST (just return the weight or the MST, whatever's easier). You can use the algorithms from class (DFS, Explore, BFS, Dijkstra's, SCC, Topological Sort) as black-box algorithms if you'd like. Explain your algorithm in words. Note the running time of your algorithm in terms of n and m. Part (a): e ∉ T and w~(e) > w(e): [Blank space for the answer] Part (b): e ∉ T and w~(e) < w(e): [Blank space for the answer] Part (c): e ∈ T and w~(e) < w(e): [Blank space for the answer] Part (d): e ∈ T and w~(e) > w(e): [Blank space for the answer]arrow_forwardQ. When we split a 4-node, we sometimes set the color of the right node to RED inrotateRight() and then immediately set it to BLACK in flipColors(). Isn’t thatwasteful?arrow_forwardLet T be a rooted tree. The height of T is 5. Every node of T has at most 3 children. How many leaves can T have at the most?arrow_forward