
Concept explainers
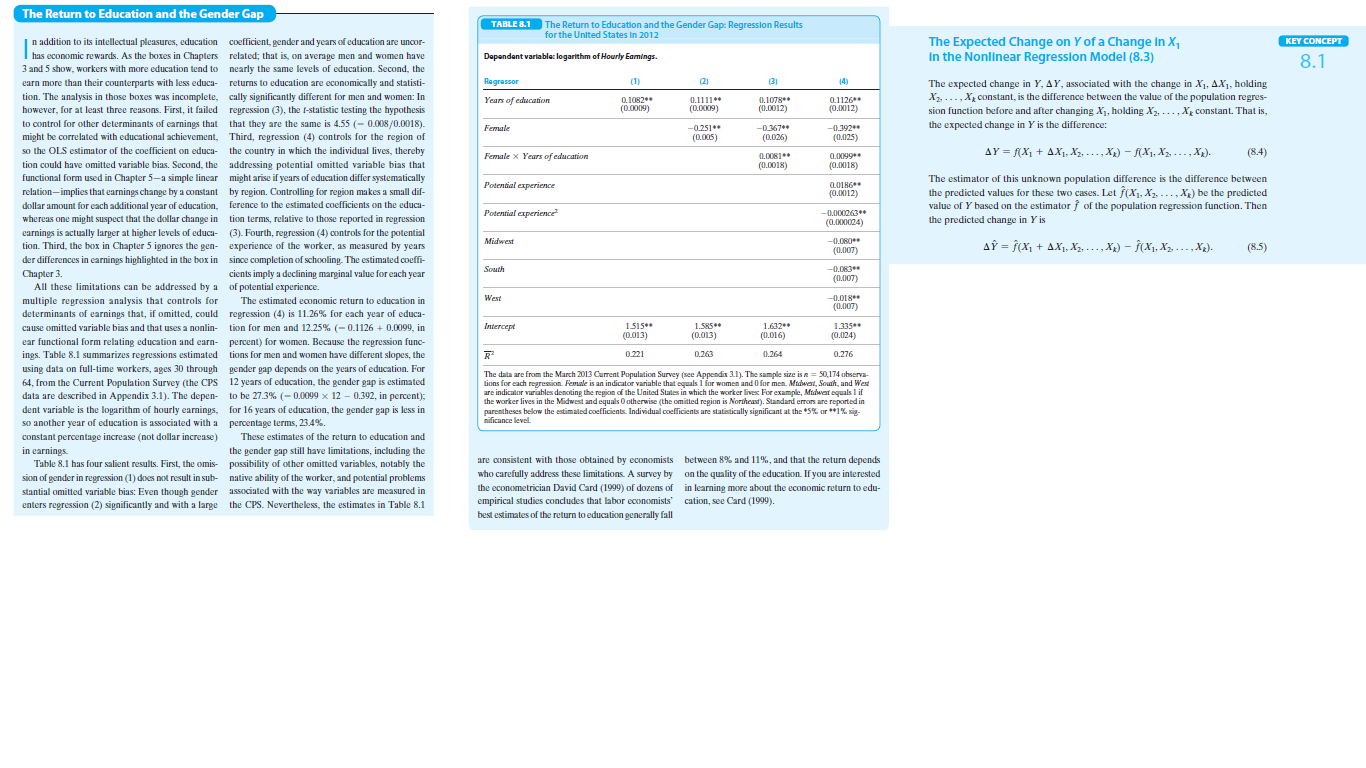
Read the box “The Return to Education and the Gender Gap”.
a. Consider a man with 16 years of education and 2 years of experience
who is from a western state. Use the results from column (4)
of Table 8.1 and the method in Key Concept 8.1 to estimate the
expected change in the logarithm of average hourly earnings (AHE)
associated with an additional year of experience.
b. Repeat (a), assuming 10 years of experience.
c. Explain why the answers to (a) and (b) are different.
d. Is the difference in the answers to (a) and (b) statistically significant
at the 5% level? Explain.
e. Would your answers to (a) through (d) change if the person were a
woman? If the person were from the South? Explain.
f. How would you change the regression if you suspected that the effect
of experience on earnings was different for men than for women?
Trending nowThis is a popular solution!
Step by stepSolved in 5 steps with 7 images

Can you also provide solutions for question d,e, and f?
d. Is the difference in the answers to (a) and (b) statistically significant
at the 5% level? Explain.
e. Would your answers to (a) through (d) change if the person were a
woman? If the person were from the South? Explain.
f. How would you change the regression if you suspected that the effect
of experience on earnings was different for men than for women?
Can you also provide solutions for question d,e, and f?
d. Is the difference in the answers to (a) and (b) statistically significant
at the 5% level? Explain.
e. Would your answers to (a) through (d) change if the person were a
woman? If the person were from the South? Explain.
f. How would you change the regression if you suspected that the effect
of experience on earnings was different for men than for women?
- Determine whether the following table shows exponential data or linear data. x 0 5 10 15 y 62 135.9 298 653.4 a) The data are linear.b) The data are exponential.arrow_forwardThe following table shows the income, measured in thousands of dollars, from sales of a certain magazine at the start of the given year. Find an exponential model for the income where I is the income, measured in thousands of dollars, and t is the number of years since 2000. Round the parameters to the nearest hundredth. Year 2000 2001 2002 2003 2004 Income 7.54 8.02 8.52 9.05 9.62 a) I = 7.54 x 1.06^tb) I = 7.51 x 0.52^tc) I = 1.06 x 7.51^td) I = 7.54 x 0.52^tarrow_forwardResearchers often rely on surveys to capture a subjective assessment of well-being. One study finds that holding everything else constant, people seem to be least happy when they are in their 40's. Another study suggests that money does buy happiness, but its effects diminishes as income rises above $75000 a year. The accompanying data file includes survey daa of 100 working adults' self-assessed happiness on a scale of ) to 100, along with their age and annual income. Estimate and interpret a regression model based on Age, Age 2 and income. Predict happiness with income equal = to $80000 and age equal to 30, 45, and 60 Years Predict happiness with Age equal = to 60 and income equal to 25,000, 75000, and 125000 Happiness Age Income 69 49 52000 83 47 123000 86 72 112000 73 52 166000 89 68 90000 81 37 152000 75 48 58000 56 48 50000 75 56 93000 57 51 27000 77 60 173000 83 55 173000 85 75 68000 82 69 157000 63 39 40000 70 66 107000 78 34 109000 53…arrow_forward
- Part D. Data from the Statistical Abstract of the United States provides a panel data collected at the state level in 1987 and 1990. These data are used to estimate MODEL 1: The variables used in the analysis are: infmort is number of deaths within the year per 1,000 live births Ipcinc is natural log of per capita income Ipopul is natural log of the population (the population is in thousands) Iphysic is natural log of physicians per 100,000 inhabitants d90 is year dummy for 1990. For questions 1 to 4 you can assume that MLR 1-4 are satisfied. A 1. Use the Stata output below to interpret ß3. Test at a 5% significance level whether the number of physicians per capita has any effect on infant mortality rate. reg infmort 1pcinc 1popul 1physic d90 Source Model Residual Total infmort infmort = Po + B₁lpcinc + B₂lpopul + ß3lphysic + 8₁ d90 + u SS 78.0499129 350.452136 428.502049 df . 19.5124782 4 97 3.61290862 Coef. Std. Err. MS 101 4.24259454 1pcinc -4.693354 1.638132 1popul - .0551426…arrow_forwardA 18.2% B 15.7% C 22.2% D 4.4%arrow_forward11. An enquiry into the budgets of middle class families in a village gave the following information : Expenses on Food 30% Rent 15% Clothing 20% Fuel 10% | Others 25% Price in Rs. in 1987 100 20 70 20 40 Prices in Rs. in 2005 90 20 60 15 55 E PW = 10101.5; E W log P = 199.494; where P = x 100. The price index number based %3D Po on Weighted Arithmetic mean of Price Relatives is : (С) 111.015 (A) 101.015 (B) 103.015 (D) 113.015.arrow_forward
- A "Student Drug Use and Health Survey" of Ontario high school students found that the percentage of students that reported serious psychosocial distress in the past month increased from 10.7% in 2013 to 17.1% in 2017. Assuming a standard exponential growth trend, what is the annual growth rate in the percentage of students reporting serious psychosocial distress in the past month?arrow_forwardA lab has been storing a radioactive substance fro a number of years. Here is a table showing the amount in grams over time. years 1960 1970 1980 1990 Amount 500 300 180 108 a) Show that the data can be modeled by an exponential function. b) Find the exponential function that models the amount of radioactive material by hand. You will need to choose your variables and identify what each represents. c) If the trend persisted, when would you expect to have 20.52 grams left?arrow_forwardPesticide danger: One of the factors that determines the degree of risk a pesticide poses to human health is the rate at which a pesticide is absorbed into skin after contact. An important question is whether the amount in the skin continues to increase with the length of the contact, or whether it increases for only a short time before leveling off. To investigate this, measured amounts of a certain pesticide were applied to 20 samples of rat skin. Four skins were analyzed at each of the time intervals 1, 2, 4, 10, and 24 hours. The amounts of the chemical (in micrograms) that were in the skin are given in the following table. Duration Amounts Absorbed 1 1.5 2.7 1.6 1.6 2 1.7 1.7 2.4 2.3 4 1.4 2.1 1.6 1.2 10 2.4 1.2 2.1 2.6 24 2.2 1.8 1.7 1.3 Send data to Excel Part: 0 / 2 Part 1 of 2 (a) Construct an ANOVA table. Round your answers to four decimal places. One-way ANOVA: Pesticide Amount Source DF SS MS F Duration Error Totalarrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





