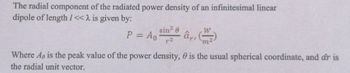
The radial component of the radiated power density of an infinitesimal linear dipole of length /<<λ is given by: P = Ao sin²8 1-2 âr, Where Ao is the peak value of the power density, is the usual spherical coordinate, and dr is the radial unit vector.

An antenna radiates a total power of 100W in the direction of maximum radiation, the field strength at a distance of 10Km was found to be 12mV/m. What is the gain of the antenna? Assume free space propagation. If η=90% find directivity.

Radius of near-field zones for various frequencies. For each frequency given in the list below, calculate the distance for which 2tr/λ=1. This distance is the approx- imate boundary between the area where magnetic and electric fields are significant, and the region where primarily radiated electromagnetic fields are present. NF (a) f=1.2 MHz (in AM broadcast band) (b) f=2GHz (computer clock rate) (c) f=60 Hz (AC power line) (d) f=116MHz (aircraft communications band).

Solve for i, using mesh analysis. 4 2 2H ll ww 10 sin (41) O 15cos(4t) 0.25 F