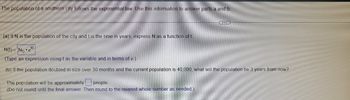
The population of a southern city follows the exponential law. Use this information to answer parts a and b T (a) If N is the population of the city and t is the time in years, express N as a function of t N(t)= No en kt (Type an expression using t as the variable and in terms of e.) (b) If the population doubled in size over 30 months and the current population is 40,000, what will the population be 3 years from now? The population will be approximately people. (Do not round until the final answer. Then round to the nearest whole number as needed.)

The graph (in the attached picture) shows four exponential functions, each with the equation; y = abx  If a > 1 and b > 1, then which of four (in the attached picture) could be its graph?

A national census bureau predicts that a certain population will increase from 35.3 million in 2000 to 64.3 million in 2060. Complete parts (a) through (c) below. (a) Find an exponential function of the form f(t) = y₁b¹ for these data, in which t= 0 corresponds to 2000 and f(t) is in millions. f(t) (Use integers or decimals for any numbers in the expression. Round to four decimal places as needed.) (b) What is the projected population in 2030? In 2040? = In 2030, the population is projected to be (Round to one decimal place as needed.) million. million. In 2040, the population is projected to be (Round to one decimal place as needed.) (c) By experimenting with different values of t (or by using a graphing calculator to solve an appropriate equation), estimate the first full year in which the population will exceed 56 million. The first full year in which the population will exceed 56 million is

In 2011, the population of Canada was about 34.34 million. For the years 2011 through 2021, the population is projected to grow at a rate of about 1.1% per year. (a) Find a formula for an exponential function that gives the population of Canada. (Let N be the population in millions and t be the number of year since 2011.) N(t) = (b) Express, using functional notation, the population of Canada in 2017. NO Calculate that value. (Round your answer to two decimal places.) million (c) Use the function you found in part (a) to predict when the population of Canada will reach 37.5 million. (Round your answer to two decimal places.) years after 2011