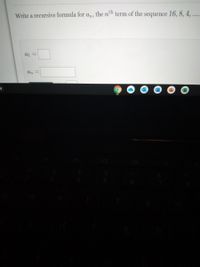
Write a recursive formula for am, the n™ term of the sequence 16, 8, 4, ....thai =an =

Answered: Image /qna-images/answer/99617c97-515f-4f05-8714-6e47d0a53f90.jpg

Answered: the nth term of the sequence 16, 8, 4,…

Math

Algebra

the nth term of the sequence 16, 8, 4, ... An Write a recursive formula for a,„, a1 = an

Algebra and Trigonometry (6th Edition)

6th Edition

ISBN:9780134463216

Author:Robert F. Blitzer

Publisher:Robert F. Blitzer

ChapterP: Prerequisites: Fundamental Concepts Of Algebra

Section: Chapter Questions

Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...

See similar textbooks

Similar questions

·.} the first term is 7 and the 14th term is 46, In an arithmetic sequence {a1, a2, A3, · · then S14 is 413 742 371 46 322
Find the first five terms of the sequence defined by the following recursive definition. a, = 13 an = an-1+4, ifn>1 How is the sequence related to the sequence a, = 4n +9? ..... The first term of the sequence defined by the recursive definition is The second term of the recursive sequence is The third term of the recursive sequence is The fourth term of the recursive sequence The fifth term of the recursive sequence is How is the recursive sequence related to the sequence a, = 4n + 9? O A. The values of the sequence defined by the recursive definition are half of the values of the sequence a, = 4n + 9. O B. The values of the sequence defined by the recursive definition are greater than the values of the sequence a, = 4n + 9. OC. The values of both the sequences are the same. D. The values of the sequence defined by the recursive definition are smaller than the values of the sequence a, = 4n +9.
A sequence {an}-1 satisfies a1 = 1, a2 = 1 and n=1 4 max {am-1, an-2} – min {an-1, an-2} An = for n > 3. Select all what applies to the sequence {an}_, from the following list. (Remember: if a > b then max{a,b} = a and min {a, b} = b) n=1 (A) Divergent (B) a1014 = 1 (C) Alternating. (D) Convergent.
1) Find the first 4 terms of each sequence: a) Un =2 +4Un-1 „U1= 3 b) Un= 4n + 2Un-1 „U1=1 c) Un=(Un-1)(Un-2) ,U1=1 and U2=2 d) Un+1 = Un + d , U1= a
Find a formula for the general term an {5, 8, 11, 14, 17, .} 5n + 3 On+3 3n + 2 O 2n + 3
Find the recursive formula of the following sequence. (4, 7, 15, 24, .} a1 = 4, an = a,n-1+ 3(n + 1), for n 22 a a1 = 4, a, = an-1+ 3(n – 1), for n 22 a1 = 4, an = a, + 3(n – 1), for n 2 2 d. a1 = 4, a, = an-1+3(n – 1), for n 2 4
Write an explicit formula and a recursive formula for the following sequence: 32, 26, 20, 14, 8,.. Your answer should be formatted in the following manner in the textbox: • 0:00 /0:11 an = Explicit: a1 lan (an = %3D Recursive: BIUA A I E E = x, E E re to search |耳

In a sequence {1, 5, 15, 35, 70, 126}, what is the recursion formula for these numbers in this sequence?
What is the recursive formula for the sequence? 4, 24, 216, 2592, 38880, ... a1 = 4, an = 3na,-1 а1 — 4, а, — 3 + паn-1 а1 — 4, аn —п+Зап-1 aj — 4, аn — пап-1 а1 3 4, а, — За, —1 — п
find the explicit formula San's n-i for the nth term of the Sequence 343,2401.. >1)-7, 니9,- . 6 an = math
Suppose that the sequence {ag}1 is 1,3, 5, 7,9, 11, 13, ... What is a1?
A sequence a1, a2, a3,.... satisfies the property that an+1 is the average of the first n terms if n=2. If a1 = 1 and a2018 = 2018, find a2,