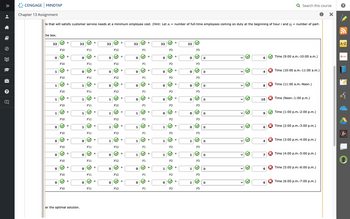
The Northside Bank is working to develop an efficient work schedule for full-time and part-time tellers. The schedule must provide for efficient operation of the bank, including adequate customer service, employee breaks, and so on. On Fridays, the bank is open from 9:00 A.M. to 7:00 P.M. The number of tellers necessary to provide adequate customer service during each hour of operation is summarized here.   Time No. of Tellers Time No. of Tellers 9:00 a.m.-10:00 a.m. 6 2:00 p.m.-3:00 p.m. 7 10:00 a.m.-11:00 a.m. 5 3:00 p.m.-4:00 p.m. 6 11:00 a.m.-Noon 7 4:00 p.m.-5:00 p.m. 8 Noon-1:00 p.m. 11 5:00 p.m.-6:00 p.m. 7 1:00 p.m.-2:00 p.m. 9 6:00 p.m.-7:00 p.m. 5   Each full-time employee starts on the hour and works a 4-hour shift, followed by a 1-hour break and then a 3-hour shift. Part-time employees work one 4-hour shift beginning on the hour. Considering salary and fringe benefits, full-time employees cost the bank $15 per hour ($105 a day), and part-time employees cost the bank $8 per hour ($32 per day).   (a) Formulate an integer programming model that can be used to develop a schedule that will satisfy customer service needs at a minimum employee cost. (Hint: Let xi = number of full-time employees coming on duty at the beginning of hour i and yj = number of part-time employees coming on duty at the beginning of hour j.)   If your answer is zero enter “0” and if the constant is "1" it must be entered in the box. 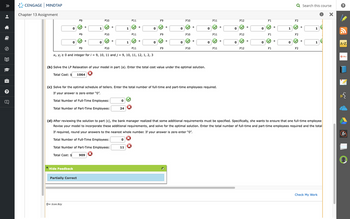(b) Solve the LP Relaxation of your model in part (a). Enter the total cost value under the optimal solution.   Total Cost: $      (c) Solve for the optimal schedule of tellers. Enter the total number of full-time and part-time employees required.   If your answer is zero enter “0”.   Total Number of Full-Time Employees:     Total Number of Part-Time Employees:       (d) After reviewing the solution to part (c), the bank manager realized that some additional requirements must be specified. Specifically, she wants to ensure that one full-time employee is on duty at all times and that there is a staff of at least four full-time employees. Revise your model to incorporate these additional requirements, and solve for the optimal solution. Enter the total number of full-time and part-time employees required and the total cost under the revised optimal solution.   If required, round your answers to the nearest whole number. If your answer is zero enter “0”.   Total Number of Full-Time Employees:     Total Number of Part-Time Employees:     Total Cost: $

Scenario Office Equipment, Inc. (OEI) leases automatic mailing machines to business customers in Fort Wayne, Indiana. The company built its success on a reputation of providing timely maintenance and repair service. Each OEI service contract states that a service technician will arrive at a customer’s business site within an average of 3 hours from the time that the customer notifies OEI of an equipment problem. Currently, OEI has 10 customers with service contracts. One service technician is responsible for handling all service calls. A statistical analysis of historical service records indicates that a customer requests a service call at an average rate of one call per 50 hours of operation. If the service technician is available when a customer calls for service, it takes the technician an average of 1 hour of travel time to reach the customer’s office and an average of 1.5 hours to complete the repair service. However, if the service technician is busy with another customer when a…

state whether or not each situation would be considered “compensable time” (and why or why not). An employee of a fast food chain has to arrive at work 15 minutes early to change into the“mascot” costume and it typically takes another 15 minutes at the end of the shift to change outof the costume and properly store it. Due to the cost of the costume, employees are notallowed to take the costume home. The “mascots” typically work from 10am – 2pm, to coverthe lunch rush periods. How much time would be “compensable” for the mascots, assumingthe conditions/schedule listed above?2) George is a Radiology Technician at a local hospital and when on call, is required to be nofurther than 30 minutes away from the facility. Is the “on call” time, compensable?

You work as the administrative manager in charge of the operations of the medical services office that brings together over 10 specialists from different health fields. Each specialist has about 5 administrative employees who help with coding, billing, customer service, and other administrative tasks. You supervise all administrative employees. For two months you have noticed that a series of conflicts have arisen between the employees you supervise, which you must address promptly to avoid escalation. These are the conflicts that have been identified: A new position has been opened to supervise night operations and two of the employees have requested it. However, both have resorted to demonstrating that the other does not have the capabilities to rise to the position. These interpersonal differences have resulted in a tense work environment.It has been rumored that one of the medical specialists is going to retire, so it is possible that he will put the five administrative employees…