MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Related questions
Concept explainers
Question
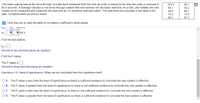
Transcribed Image Text:The text describes a study conducted at a fast-food restaurant to evaluate a new drive-through system designed to reduce wait times. The existing mean waiting time is 84.4 seconds. The manager tests the new system by measuring wait times for 10 randomly selected orders. The recorded times are:
- 103.4
- 82.1
- 66.1
- 93.2
- 58.5
- 86.1
- 74.2
- 72.6
- 66.1
- 87.7
**Hypotheses:**
- Null hypothesis (\(H_0\)): The mean wait time is 84.4 seconds.
- Alternative hypothesis (\(H_1\)): The mean wait time is less than 84.4 seconds.
**Task:**
1. **Find the Test Statistic (\(t_0\)):**
- Round to two decimal places as needed.
2. **Find the P-value:**
- Round to three decimal places as needed.
3. **Conclusion Using Significance Level \( \alpha = 0.1 \):**
Choose from the following options:
- **A.** The P-value is less than the level of significance, so there is sufficient evidence to conclude the new system is effective.
- **B.** The P-value is greater than the level of significance, so there is not sufficient evidence to conclude the new system is effective.
- **C.** The P-value is less than the level of significance, so there is not sufficient evidence to conclude the new system is effective.
- **D.** The P-value is greater than the level of significance, so there is sufficient evidence to conclude the new system is effective.
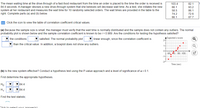
Transcribed Image Text:The text provided is part of an educational exercise involving hypothesis testing and the analysis of waiting times at a fast-food restaurant. A manager believes a new drive-through system will reduce wait times, and data from 10 orders are provided for analysis.
**Table of Wait Times (in seconds):**
- 103.4, 82.1
- 66.1, 93.2
- 58.5, 86.1
- 74.2, 72.6
- 66.1, 87.7
**Analysis Steps:**
### (a) Verification of Conditions
- **Objective:** Verify that wait times are normally distributed and free of outliers.
- **Data Check:** A normal probability plot is provided with a sample correlation coefficient \( r = 0.989 \).
- **Analysis:**
- **Conditions Satisfied?** The text prompts to check two conditions using drop-down selections.
- **Interpretation of Plot:** The probability plot is described as linear enough due to the high correlation coefficient (\( r = 0.989 \)).
- **Boxplot:** No outliers are present.
### (b) Hypothesis Testing for System Effectiveness
- **Objective:** Determine if the new system effectively reduces wait times using the P-value approach at a significance level \(\alpha = 0.1\).
- **Hypotheses Setup:**
- Null Hypothesis (\( H_0 \)): \(\mu = 84.4\)
- Alternative Hypothesis (\( H_1 \)): \(\mu < 84.4\)
- **Task:** Find the test statistic using the provided options.
**Graph Explanation:**
- **Normal Probability Plot:** This graph plots expected z-scores against actual time data, showing a linear trend which supports normal distribution.
This exercise involves statistical understanding to determine the effectiveness of operational changes in reducing service times.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- In some 4.0 grading systems, a student's grade point aversge (GPA) is calculated by assigning letter grades the following numerical values. (See attachment) Use this grading system to find this student's GPA. Round to the nearest hundredth. Tessa's cumulative GPA for 3 semesters was 3.18 for 46 course units. Her fourth semester GPA was 3.72 for 12 course units. What is Tessa's cumulative GPA for all 4 semesters?arrow_forwardIs the average time to complete an obstacle course longer when a patch is placed over the right eye than when a patch is placed over the left eye? Thirteen randomly selected volunteers first completed an obstacle course with a patch over one eye and then completed an equally difficult obstacle course with a patch over the other eye. The completion times are shown below. "Left" means the patch was placed over the left eye and "Right" means the patch was placed over the right eye. Time to Complete the Course Right 43 42 45 43 42 43|| 44 44 Left 42 42 47|| 41 42 43 46 || 44 Assume a Normal distribution. What can be concluded at the the a = 0.01 level of significance level of significance? For this study, we should use Select an answer a. The null and alternative hypotheses would be: Ho: Select an answer v Select an answer v Select an answer v (please enter a decimal) H: Select an answer v Select an answer v| Select an answer v (Please enter a decimal) b. The test statistic ? v (please…arrow_forwardYou want to determine how many loaves of Bread are sold per day at Schat’s Bakery. You stand outside for ten different randomly selected days, count the number of loaves, and then average them. You come up with 421 loaves per day. In reality, Schat’s keeps records of how many loaves they sell per day, and in they averaged 395 loaves per day. Describe what the population is in the above example?arrow_forward
- For letter B please plug in the number 6arrow_forwardA 10-yr-old competes in gymnastics. For several competitions she received the following "All-Around" scores: 36, 35.1, 38.3, and 37.8. Her coach recommends that gymnasts whose "All-Around" scores average at least 38.3 move up to next level. What "All-Around" scores in the next competition would result in the child being eligible to move up? 2151 0818 The child needs a score of at least Recheck 89°F Partly sunny * Try again $ 14 10 ts % - ▼ to move up to next level of competition. Q Search 6 & 7 LOO 4+ 8 fo 144 9 X f10 11 3 Submit Assignm Ⓒ2023 McGraw Hill LLC. All Rights Reserved. Terms of Use | Privacy Center | Acces @45 O 4 5 + prt sc ENG delete 30arrow_forwardLee walked 1000 steps Monday, 3000 steps Tuesday, 3000 steps Wednesday, and 1000 steps Thursday. What is Lee's average daily steps?arrow_forward
- solve for UCLparrow_forwardA 10-yr-old competes in gymnastics. For several competitions she received the following "All-Around" scores: 36.9, 35.4, 38.6, and 35.2. Her coach recommends that gymnasts whose "All-Around" scores average at least 38.1 move up to next level. What "All-Around" scores in the next competition would result in the child being eligible to move up? The child needs a score of (Choose one) V to move up to next level of competition.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning 
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning
Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON
The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman