
Database System Concepts
7th Edition
ISBN: 9780078022159
Author: Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Question
The greatest common divisor of two positive integers, A and B, is the largest number that can be evenly divided into both of them. Euclid's algorithm can be used to find the greatest common divisor (GCD) of two positive integers. You can use this algorithm in the following manner:
1. Compute the remainder of dividing the larger number by the smaller number.
2. Replace the larger number with the smaller number and the smaller number with the
remainder.
3. Repeat this process until the smaller number is zero.
The larger number at this point is the GCD of A and B. Write a program that lets the user enter two integers and then prints each step in the process of using the Euclidean algorithm to find their
GCD.
An example of the program input and output is shown below:
Enter the smaller number: 5
Enter the larger number: 15
The greatest common divisor is 5
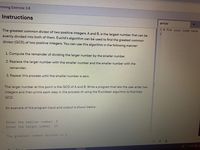
Transcribed Image Text:mming Exercise 3.8
Instructions
gcd.py
The greatest common divisor of two positive integers, A and B, is the largest number that can
1 # Put your code here
evenly divided into both of them. Euclid's algorithm can be used to find the greatest common
divisor (GCD) of two positive integers. You can use this algorithm in the following manner:
1. Compute the remainder of dividing the larger number by the smaller number.
2. Replace the larger number with the smaller number and the smaller number with the
remainder.
3. Repeat this process until the smaller number is zero.
The larger number at this point is the GCD of A and B. Write a program that lets the user enter two
integers and then prints each step in the process of using the Euclidean algorithm to find their
GCD.
An example of the program input and output is shown below:
Enter the smaller number: 5
Enter the larger number: 15
The greatest common divisor is 5
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- Using a Java program solve the following problem using arrays: Past A: Coupon collector is a classic statistic problem with many practical applications. The problem is to pick objects from a set of objects repeatedly and determine how many picks are needed for all the objects to be picked at least once. A variation of the problem is to pick cards from a shuffled deck of 52 cards repeatedly and find out how many picks are needed before you see one of each suit. Assume a picked card is placed back in the deck before picking another. Write a program to simulate the number of picks needed to get total of four cards from each different suit and display the four cards picked (it is possible that a card may be picked twice). Here is a sample run of the program: Queen of Spades 5 of Clubs Queen of Hearts 4 of Diamonds Number of picks: 12 Sample run explanation: As you see in the above run, 12 picks are made to get the four cards from different suits. The other 8 picks (12-4-8) were from the…arrow_forward1. Write a recursive method expFive(n) to compute y=5^n. For instance, if n is 0, y is 1. If n is 3, then y is 125. If n is 4, then y is 625. The recursive method cannot have loops. Then write a testing program to call the recursive method. If you run your program, the results should look like this: > run RecExpTest Enter a number: 3 125 >run RecExpTest Enter a number: 3125 2. For two integers m and n, their GCD(Greatest Common Divisor) can be computed by a recursive function. Write a recursive method gcd(m,n) to find their Greatest Common Divisor. Once m is 0, the function returns n. Once n is 0, the function returns m. If neither is 0, the function can recursively calculate the Greatest Common Divisor with two smaller parameters: One is n, the second one is m mod n. Although there are other approaches to calculate Greatest Common Divisor, please follow the instructions in this question, otherwise you will not get the credit. Meaning your code needs to follow the given algorithm. Then…arrow_forward1. Both mergesort and quicksort uses divide and conquer paradigm to sort unsorted list. (a) Imagine you want to write the quicksort algorithm to sort an array into non-increasing order. Write down the partition algorithm that is used in the divide phase in the quicksort algorithm. Show that the time complexity of this algorithm is 0(n). (b) Identify the worst case situation in the naive quicksort algorithm and show that in the worst case situation its time complexity is O(n2)arrow_forward
- There is more than one way to calculate the value of T. One way that this can be done is by generating random numbers. This works by recognizing that if you take a unit square that you can draw a quarter circle of unit radius inside the square. The area of the quarter circle is exactly π/4 and the area of the square is 1. So if you randomly generate a pair of uniform numbers between 0 and 1 they will be distributed uniformly across the square. If you count the total number of points generated and the number of points (x, y) where x² + y² = ² < 1 then the ratio of those two numbers will tend towards the ratios of the areas of the square and the circle as the number of points generated increases. The ratio of the areas is just π/4 so if you take that ratio and multiply it by 4 you get an estimate for . a) b Write code to estimate π using this method. You can generate random numbers in the range 0arrow_forwardGiven a positive integer 'n', find and return the minimum number of steps that 'n' has to take to get reduced to 1. You can perform any one of the following 3 steps:1.) Subtract 1 from it. (n = n - 1) ,2.) If its divisible by 2, divide by 2.( if n % 2 == 0, then n = n / 2 ) ,3.) If its divisible by 3, divide by 3. (if n % 3 == 0, then n = n / 3 ). Write brute-force recursive solution for this.Input format :The first and the only line of input contains an integer value, 'n'.Output format :Print the minimum number of steps.Constraints :1 <= n <= 200 Time Limit: 1 secSample Input 1 :4Sample Output 1 :2 Explanation of Sample Output 1 :For n = 4Step 1 : n = 4 / 2 = 2Step 2 : n = 2 / 2 = 1 Sample Input 2 :7Sample Output 2 :3Explanation of Sample Output 2 :For n = 7Step 1 : n = 7 - 1 = 6Step 2 : n = 6 / 3 = 2 Step 3 : n = 2 / 2 = 1 SolutionDp///.arrow_forwardGiven a positive integer 'n', find and return the minimum number of steps that 'n' has to take to get reduced to 1. You can perform any one of the following 3 steps:1.) Subtract 1 from it. (n = n - 1) ,2.) If its divisible by 2, divide by 2.( if n % 2 == 0, then n = n / 2 ) ,3.) If its divisible by 3, divide by 3. (if n % 3 == 0, then n = n / 3 ). Write brute-force recursive solution for this.Input format :The first and the only line of input contains an integer value, 'n'.Output format :Print the minimum number of steps.Constraints :1 <= n <= 200 Time Limit: 1 secSample Input 1 :4Sample Output 1 :2 Explanation of Sample Output 1 :For n = 4Step 1 : n = 4 / 2 = 2Step 2 : n = 2 / 2 = 1 Sample Input 2 :7Sample Output 2 :3Explanation of Sample Output 2 :For n = 7Step 1 : n = 7 - 1 = 6Step 2 : n = 6 / 3 = 2 Step 3 : n = 2 / 2 = 1 SolutionDp///.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education

Database System Concepts
Computer Science
ISBN:9780078022159
Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:McGraw-Hill Education

Starting Out with Python (4th Edition)
Computer Science
ISBN:9780134444321
Author:Tony Gaddis
Publisher:PEARSON

Digital Fundamentals (11th Edition)
Computer Science
ISBN:9780132737968
Author:Thomas L. Floyd
Publisher:PEARSON

C How to Program (8th Edition)
Computer Science
ISBN:9780133976892
Author:Paul J. Deitel, Harvey Deitel
Publisher:PEARSON

Database Systems: Design, Implementation, & Manag...
Computer Science
ISBN:9781337627900
Author:Carlos Coronel, Steven Morris
Publisher:Cengage Learning

Programmable Logic Controllers
Computer Science
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education