
Algebra and Trigonometry (6th Edition)
6th Edition
ISBN: 9780134463216
Author: Robert F. Blitzer
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
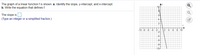
solve for a. and b.
Transcribed Image Text:### Educational Content on Linear Functions
#### The Graph of a Linear Function
The graph of a linear function \( f \) is shown below.
##### Tasks:
1. **Identify the slope, y-intercept, and x-intercept.**
2. **Write the equation that defines \( f \).**
**Identifying Key Features:**
- The slope is \( \boxed{-1} \).
*(Type an integer or a simplified fraction.)*
**Graph Explanation:**
The graph displayed is a Cartesian coordinate plane with both x and y axes ranging from -10 to 10. The linear function graph is a straight line that intersects the y-axis at \( y = 8 \) and the x-axis at \( x = 8 \).
**Steps to Identify:**
1. **Slope (m):**
- The slope of a line is calculated using the formula \( \frac{\Delta y}{\Delta x} \).
- On the graph, the line goes down by 8 units vertically (change in \( y \)) for every 8 units it moves horizontally (change in \( x \)), giving a slope of \( \frac{-8}{8} = -1 \).
2. **Y-intercept (b):**
- The y-intercept is the point where the line crosses the y-axis. On this graph, the y-intercept is at \( y = 8 \).
3. **X-intercept:**
- The x-intercept is the point where the line crosses the x-axis. On this graph, the x-intercept is at \( x = 8 \).
**Writing the Equation of the Line:**
- For a linear function in the form \( y = mx + b \):
- Given the slope \( m = -1 \) and the y-intercept \( b = 8 \),
- The equation defining \( f \) is \( y = -x + 8 \).
By understanding these key elements, students can better grasp the properties and equations of linear functions.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education