Question
The graph below shows the angular position as a function of time for a simple pendulum that is oscillating in a gravitational field with g=9.81m/s^2
Part a) calculate the amplitude in radians
Part b)find the equation for the angular position as a function of time theta(t).
Part c) find the equation for the angular velocity as a function of time omega(t).
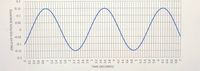
Transcribed Image Text:TIME (SECONDS)
ANGULAR POSITION (RADIANS)
0.2
0.4
0.6
0.8
1.
1.2
1.4
1.6
18
2.2
2.4
2.6
2.8
3.2
3.4
3.8
4.2
4.4
4.6
48
5.2
54
5.6
5.8
9.
6.2
6.4
6.6
6.8
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps with 4 images

Knowledge Booster
Similar questions
- Two pendula are shown in the figure. Each consists of a solid ball with uniform density and has a mass M. They are each suspended from the ceiling with massless rod as shown in the figure. The ball on the left pendulum is very small. The ball of the right pendulum has radius 1/2 L. L = 1.6 m Find the period T of the left pendulum for small displacements in s. Find the period T of the right pendulum for small displacements in s.arrow_forward5 kilogram object is suspended from a string. The string is 4 meters long. What is the period of the object ting as a pendulum? Express your answer a number of seconds, omitting the unit.arrow_forwardA point rotates about the origin in the ?? plane at a constant radius of 0.266 m with an angular velocity of 8.01 rad/s. The projection of this point's motion on the ?- or ?-axis is simple harmonic. What is the amplitude of the projected simple harmonic motion? What is the projected motion's frequency? What is the projected motion's period?arrow_forward
- For a simple pendulum, the restoring "force" is the torque due to gravity, mgL. Here m is the mass of the pendulum, g is the acceleration due to gravity, and L is the length of the pendulum. The "inertia" is the rotational inertia, mL². What is the expected period T of a simple pendulum? OA. 2л√/mg/L OB. 2√✓/L/mg OC. 2n√L/g OD. 2n√g/L OE. none of thesearrow_forwardA point rotates about the origin in the ?? plane at a constant radius of 0.211 m with an angular velocity of 9.01 rad/s. The projection of this point's motion on the ?- or ?-axis is simple harmonic. What is the amplitude of the projected simple harmonic motion? What is the projected motion's frequency? What is the projected motion's period?arrow_forwardFerris Wheel The height h (in feet) above groundof a seat on a Ferris wheel at time t (in seconds) ismodeled byh(t) = 53 + 50 sin(π10t − π2).(a) Find the period of the model. What does the periodtell you about the ride?(b) Find the amplitude of the model. What does theamplitude tell you about the ride?(c) Use a graphing utility to graph one cycle of the model.arrow_forward
- PRACTICE IT Use the worked example above to help you solve this problem. A 0.545 kg object connected to a light spring with a spring constant of 19.0 N/m oscillates on a frictionless horizontal surface. (a) Calculate the total energy of the system and the maximum speed of the object if the amplitude of the motion is 3.00 cm. E = J m/s V max = (b) What is the velocity of the object when the displacement is 2.00 cm? ± m/s (c) Compute the kinetic and potential energies of the system when the displacement is 2.00 cm. KE = J J PES= EXERCISE For what values of x is the speed of the object 0.14 m/s? x = ± cm HINTS: GETTING STARTED I I'M STUCK!arrow_forwardThe equations used to describe the physical pendulum will lead us directly to an answer. Part 3 of 3 - Analyze We are givenf = 0.685 Hz, d 0.510 m, and m = 2.10 kg. We have the following equation for the period. T = 2n V mgd This gives 4721 T2 = mgd and, solving for the moment of inertia, we have the following. T?mgd mgd %3D kg )(9.80 m/s?) m Hz kg - m2 Submit Skip (you cannot come back) Need Help? Read it O Show My Work (Optional) ?arrow_forward
arrow_back_ios
arrow_forward_ios