Question
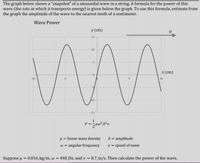
Transcribed Image Text:The graph below shows a "snapshot" of a sinusoidal wave in a string. A formula for the power of this
wave (the rate at which it transports energy) is given below the graph. To use this formula, estimate from
the graph the amplitude of the wave to the nearest tenth of a centimeter.
Wave Power
y (cm)
15
10
x (cm)
-10
5
10
10
-15
1
u = linear mass density
w = angular frequency
A = amplitude
v = speed of wave
Suppose u = 0.016 kg/m, w = 440_Hz, and v = 8.7 m/s. Then calculate the power of the wave.
%3D
%3D
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps

Knowledge Booster
Similar questions
- A 28kg block is suspended from the ceiling using thin rope (0.009 kg/m). The rope is plucked, sending a wave down the rope. Calculate the speed of the wave as it moves along the rope.arrow_forwardDon't use chat gpt plzarrow_forwardThe drawing 0.50 m A shows a graph of Amplitude (m) versus Position (m) of two waves traveling to the right at the same speed. 0.25 m x (m) 2.0 4.0 6.0 (a) Using the data in the drawing, determine the wavelength of each wave. Provide your reasoning. -0.25 m- -0.50 m (b) The speed of the waves is 15 m/s. Calculate the frequency of each one.arrow_forward
- What is the difference in motion between a transverse and longitudinal wave? Which type(s) can be considered as having kinetic energy?arrow_forwardThe speed of a sinusoidal wave on a string depends on: O the amplitude of the wave the frequency of the wave the tension in the string (the wavelength of the wavearrow_forwardA wave is created in an elastic rope. The diagram below represents a snapshot of the wave at a given time instant of time. The distance from point A to points B and C are given. Point A on the wave moves to the position of point C in 2.30 seconds. Determine the wavelength (in meters), frequency (in Hertz), and speed (in meters/second) of this wave.arrow_forward
- A harmonic wave is traveling along a rope. It is observed that 30 complete waves pass every 25 seconds. Also, the distance the wave travels is 5.0 m in 8.0 seconds. What is the wavelength?arrow_forwardThe wave show is vibrating with a frequency of 250 Hz. If the length of the string is 2.00 m what is the velocity of the wave? vibrator amplitude mass O 167 m/s 125 m/s 500 m/s O 333 m/s LHarrow_forwardQUESTION 1 Problem #1: A wave is modeled by the wave function below. What is the amplitude, wavelength, wave speed, period, and frequency of the wave? y (x, t) = (0.50 cm)sin (1.57 m-lr - 6.28 s-1t)arrow_forward
- A nylon rope of length 25m is under a tension of 1.3 × 104 N. The total mass of this rope is 2 kg. If a wave pulse starts at one end of this rope, find its speed. Calculate to one decimals?arrow_forwardWhat mathematical relationship exists between the wave speed and and the tension of the medium according to the POWER trendline equation from the graph? Be specific with the answer (i.e., describe the full mathematica proportionality between the two variables) Feel free to use the graph. Table: Frequency (Hz) Density (kg/m) Tension (N) Speed (cm/s) Wavelength (cm) 0.75 1.0 2.0 141.4 188.53 0.75 1.0 2.5 158.1 210.8 0.75 1.0 3.0 173.2 230.93 0.75 1.0 3.5 187.1 249.47 0.75 1.0 4.0 200 266.67arrow_forward
arrow_back_ios
arrow_forward_ios