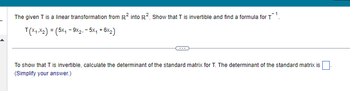
The given T is a linear transformation from R² into R². Show that T is invertible and find a formula for T¹. T(x₁.x2) = (5x₁9x2,- 5x₁ + 6x₂) To show that T is invertible, calculate the determinant of the standard matrix for T. The determinant of the standard matrix is (Simplify your answer.)

The determinant of which of the matrices below needs to be found to determine Dx for this system of equations. 2x - 3y = 17 5x + 4y = 8 Select one: O a. O b. None of these (3 ( 31 [²¹7] O C. (473) O d.

a []·. and 0, and compute the determinants of the matrices [u v] and [vu]. Draw a picture and explain what you find. Let u = C [:] , where a, b, and c are positive (for simplicity). Compute the area of the parallelogram determined by u, v, u + v, 0 and v= The area of the parallelogram determined by u, v, u + v, and 0 is (Simplify your answer.)

Compute the determinant of the following matrix. You must show your work, and may want to use properties of determinants to simplify the work you need to do. 4 3 1-3 8 1 92 0647 12 0 3 -2