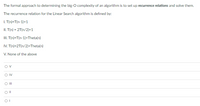
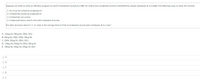
The formal approach to determining the big-O complexity of an algorithm is to set up recurrence relations and solve them.The recurrence relation for the Linear Search algorithm is defined by:I. T(n)=T(n-1)+1II. T(n) = 2T(n/2)+1II. T(n)=T(n-1)+Theta(n)IV. T(n)=2T(n/2)+Theta(n)V. None of the aboveOvOII Suppose we need to write an efficient program to store N employee records for ABC Inc where each employee record is identified by unique employee id. Consider the following ways to store the records.1. An array list sorted by employee id2. A linked list sorted by employee id3. A linked list not sorted4. A balanced binary search tree with employee id as keyFor data structure above in 1-4, what is the average time to fınd an employee record given employee id as a key?A. O(log N), O(log N), O(N), O(1)B. O(log N), O(N), O(N), O(log N)C. O(N), O(log N). O(N), O(1)D. O(log N), O(log N), O(N), O(log N)E. O(log N), O(log N), O(log N), O(1)O AO DO EO B

- We need to choose for the recurrence of linear search and other time complexity in employee id…

The formal approach to determining the big-O complexity of an algorithm is to set up recurrence relations and solve them. The recurrence relation for the Linear Search algorithm is defined by: I. T(n)=T(n-1)+1 II. T(n) = 2T(n/2)+1 II. T(n)=T(n-1)+Theta(n) IV. T(n)=2T(n/2)+Theta(n) V. None of the above Ov O II

The formal approach to determining the big-O complexity of an algorithm is to set up recurrence relations and solve them. The recurrence relation for the Linear Search algorithm is defined by: I. T(n)=T(n-1)+1 II. T(n) = 2T(n/2)+1 II. T(n)=T(n-1)+Theta(n) IV. T(n)=2T(n/2)+Theta(n) V. None of the above Ov O II

Database System Concepts

7th Edition

ISBN:9780078022159

Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan

Publisher:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan

Chapter1: Introduction

Section: Chapter Questions

Problem 1PE

See similar textbooks

Similar questions

Code req positive integer decompose, find an algorithm to find the number ofnon-negative number division, or decomposition. The complexity is O(n^2). Example 1:Input: 4Output: 5Explaination:4=44=3+14=2+24=2+1+14=1+1+1+1 Example :Input: 7Output: 15Explaination:7=77=6+17=5+27=5+1+17=4+37=4+2+17=4+1+1+17=3+3+17=3+2+27=3+2+1+17=3+1+1+1+17=2+2+2+17=2+2+1+1+17=2+1+1+1+1+17=1+1+1+1+1+1+1.
Suppose you have an algorithm that operates on a set of data with n elements. If the recurrence formula that computes the time requirement for the algorithm is given by T(n) = 87 (C (1) + Dn a. nlgn b. n² lg n c. n² d. n³ e. if n > 1 if n = 1 where D and C are constants, which of the following gives the order of complexity of the algorithm? none of the other answers
1. Determine the running time of the following algorithm. Write summations to represent loops and solve using bounding. Be sure to show work on both the upper bound and lower bound, justify the split, and check that the bounds differ by only a constant factor. Use asymptotic notation to write the answer. Func1(n) 1 2 3 4 5 6 7 8 9 10 11 S← 0; for i ←n to n² do for j← 1 to i do for k9n to 10n² do for mi to k end end end return (s); end s+s + i- j + k −m;
Solving recurrences using the Substitution method. Give asymptotic upper and lower bounds for T(n) in each of the following recurrences. Solve using the substitution method. Assume that T(n) is constant n ≤ 2. Make your bounds as tight as possible and justify your answers. Hint: You may use the recursion trees or Master method to make an initial guess and prove it through induction a. T(n) = 2T(n-1) + 1 b. T(n) = 8T(n/2) + n^3
Time comp.
Consider the following algorithm that uses a sorted list of n elements (alist). What is the worst case runtime of this algorithm? for each element in alist 1. ask the user for an input, call it value 2. search value in alist using binary search 3. if value exists in alist, print "successful" otherwise print "unsuccessful" Question options: a. O(log n) b. O(n) c. O(n log n) d. O(2^n) e. O(n^2) f. O(1)
Arrange this functions in increasing order of asymptotic complexity Select one: a. f1, f2, f3 b. f2, f1, f3 c. f2, f3, f1
Solve the following recurrences using recursion tree method and write the asymptotic time-complexity. 1. T(n) = 3T (n/4) + n^22. T(n) = T (n/5) + T(4n/5) + n3. T(n) = 3T(n − 1) + n^4 4. T(n) = T (n/2) + n^2
Consider the following recursive algorithm, where // denotes integer division: 3//2 = 1, 5//2 = 2, etc. F(n):if n <= 1: returnF(n//2)for i from 0 to n for j from 0 to n//2 print(i+j) Let function T(n) denote the running time of this algorithm. Derive T(n) and prove its worst case timecomplexity
I was told the answer is (n lg n) but I am not sure.
Use a recursion tree to determine a good asymptotic upper bound on the recurrence T(n)=4T(n/2+2)+n. Use the substitution method to verify your answer.
Use the recursion tree method to solve the following recurrence T(n) by finding the tightest function f(n) such that T(n) = O(f(n)). T(n) ≤ 4.T(n/3) +0(n³)