
C++ for Engineers and Scientists
4th Edition
ISBN: 9781133187844
Author: Bronson, Gary J.
Publisher: Course Technology Ptr
expand_more
expand_more
format_list_bulleted
Question
Please sttae clearly what should I choose from the multiple choice
Thanks so much
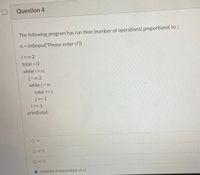
Transcribed Image Text:Question 4
The following program has run time (number of operations) proportional to :
n = int(input("Please enter n"))
i = n-2
total = 0
%3D
while i < n:
j = n-2
while j< n:
total += j
j+= 1
i+= 1
print(total)
On
O n^2
O n^3
constant (independant of n)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- A(n) __________ contains 8 __________.arrow_forward(Program) Write a program that tests the effectiveness of the rand() library function. Start by initializing 10 counters, such as zerocount, onecount, twocount, and so forth, to 0. Then generate a large number of pseudorandom integers between 0 and 9. Each time 0 occurs, increment zerocount; when 1 occurs, increment onecount; and so on. Finally, display the number of 0s, 1s, 2s, and so on that occurred and the percentage of time they occurred.arrow_forward(Electrical eng.) a. An engineer has constructed a two-dimensional array of real numbers with three rows and five columns. This array currently contains test voltages of an amplifier. Write a C++ program that interactively inputs 15 array values, and then determines the total number of voltages in these ranges: less than 60, greater than or equal to 60 and less than 70, greater than or equal to 70 and less than 80, greater than or equal to 80 and less than 90, and greater than or equal to 90. b. Entering 15 voltages each time the program written for Exercise 7a runs is cumbersome. What method could be used for initializing the array during the testing phase? c. How might the program you wrote for Exercise 7a be modified to include the case of no voltage being present? That is, what voltage could be used to indicate an invalid voltage, and how would your program have to be modified to exclude counting such a voltage?arrow_forward
- A(n) __________ is an array of characters.arrow_forward(Data processing) The answers to a true-false test are as follows: T T F F T. Given a twodimensional answer array, in which each row corresponds to the answers provided on one test, write a function that accepts the two-dimensional array and number of tests as parameters and returns a one-dimensional array containing the grades for each test. (Each question is worth 5 points, so the maximum possible grade is 25.) Test your function with the following data:arrow_forward(Statistics) a. Write a C++ program that reads a list of double-precision grades from the keyboard into an array named grade. The grades are to be counted as they’re read, and entry is to be terminated when a negative value has been entered. After all grades have been input, your program should find and display the sum and average of the grades. The grades should then be listed with an asterisk (*) placed in front of each grade that’s below the average. b. Extend the program written for Exercise 1a to display each grade and its letter equivalent, using the following scale: Between90and100=AGreaterthanorequalto80andlessthan90=BGreaterthanorequalto70andlessthan80=CGreaterthanorequalto60andlessthan70=DLessthan60=Farrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr
C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage LearningProgramming Logic & Design ComprehensiveComputer ScienceISBN:9781337669405Author:FARRELLPublisher:Cengage
C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage LearningProgramming Logic & Design ComprehensiveComputer ScienceISBN:9781337669405Author:FARRELLPublisher:Cengage Microsoft Visual C#Computer ScienceISBN:9781337102100Author:Joyce, Farrell.Publisher:Cengage Learning,
Microsoft Visual C#Computer ScienceISBN:9781337102100Author:Joyce, Farrell.Publisher:Cengage Learning, Systems ArchitectureComputer ScienceISBN:9781305080195Author:Stephen D. BurdPublisher:Cengage Learning
Systems ArchitectureComputer ScienceISBN:9781305080195Author:Stephen D. BurdPublisher:Cengage Learning EBK JAVA PROGRAMMINGComputer ScienceISBN:9781337671385Author:FARRELLPublisher:CENGAGE LEARNING - CONSIGNMENT
EBK JAVA PROGRAMMINGComputer ScienceISBN:9781337671385Author:FARRELLPublisher:CENGAGE LEARNING - CONSIGNMENT

C++ for Engineers and Scientists
Computer Science
ISBN:9781133187844
Author:Bronson, Gary J.
Publisher:Course Technology Ptr

C++ Programming: From Problem Analysis to Program...
Computer Science
ISBN:9781337102087
Author:D. S. Malik
Publisher:Cengage Learning

Programming Logic & Design Comprehensive
Computer Science
ISBN:9781337669405
Author:FARRELL
Publisher:Cengage

Microsoft Visual C#
Computer Science
ISBN:9781337102100
Author:Joyce, Farrell.
Publisher:Cengage Learning,

Systems Architecture
Computer Science
ISBN:9781305080195
Author:Stephen D. Burd
Publisher:Cengage Learning

EBK JAVA PROGRAMMING
Computer Science
ISBN:9781337671385
Author:FARRELL
Publisher:CENGAGE LEARNING - CONSIGNMENT