Question
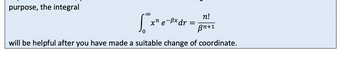
Transcribed Image Text:purpose, the integral
[ ²x² e-Pxdr = 3²
0
will be helpful after you have made a suitable change of coordinate.
n!
Bn+1

Transcribed Image Text:The expectation value, (r), for a hydrogen atom in the 3d₂2 orbital can be written
∞
4
r
= [² dr r² (2) * e-2r/3a0
(r) =
=
8
(3⁹.5) a ³
where the integrals over 0 and have already been evaluated and included in this
expression.
(a) Starting with the integral shown above, define x = r/ao and use this to simplify this
integral by expressing it as an integration over x. Be careful and don't forget about the
volume element and the integration limits.
(b) From part (a), you should now have an integral over x and this variable essentially
represents the radial distance of the electron in units of do. Determine (r) for this state.
You may find the tabulated integral given above (before problem 3) helpful.
(c) The angular part of the 3d₂2 orbital is given by the spherical harmonic, Y₂ (0,4):
5
-√√
16π
Y₂ (0,0) =
(3 cos² 0 - 1)
Using the standard limits of these variables (0 ≤ 0≤ л; 0≤ ≤ 2π), determine the angles
at which this function has nodes.
(d) Describe the nodal surfaces for the orbital, as defined by the values of the angles where
Y₂ (0,4) is zero. In other words, identify the locations and types of the angular nodal
surfaces in the Cartesian axis system.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps

Knowledge Booster
Similar questions
- (4) Electronic energy level of a hydrogen atom is given by R ; п %3D 1,2, 3,... n2 E = - and R = 13.6 eV. Each energy level has degeneracy 2n2 (degeneracy is the number of equivalent configurations associated with the energy level). (a) Derive the partition function for a hydrogen atom at a constant temperature. (b) Consider that the energy level of a hydrogen atom is approximated by a two level system, n = 1,2. Estimate the mean energy at 300 K.arrow_forwardAn electron in a hydrogen atom is approximated by a one-dimensional infinite square well potential. The normalised wavefunction of an electron in a stationary state is defined as *(x) = √√ sin (""). L where n is the principal quantum number and L is the width of the potential. The width of the potential is L = 1 x 10-¹0 m. (a) Explain the meaning of the term normalised wavefunction and why normalisation is important. (b) Use the wavefunction defined above with n = 2 to determine the probability that an electron in the first excited state will be found in the range between x = 0 and x = 1 × 10-¹¹ m. Use an appropriate trigonometric identity to simplify your calculation. (c) Use the time-independent Schrödinger Equation and the wavefunction defined above to find the energies of the first two stationary states. You may assume that the electron is trapped in a potential defined as V(x) = 0 for 0≤x≤L ∞ for elsewhere.arrow_forwardExplain each steparrow_forwardarrow_back_iosarrow_forward_ios