
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Solve correctly write the domain and range of h using interval notation
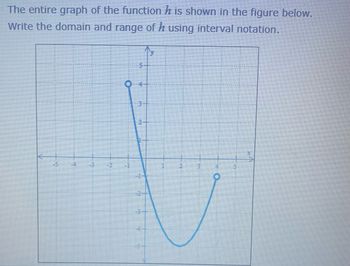
Transcribed Image Text:The text provided is:
"The entire graph of the function \(h\) is shown in the figure below. Write the domain and range of \(h\) using interval notation."
### Graph Description:
The graph is displayed on a coordinate plane with the x-axis and y-axis marked. Here are the details:
- **Domain**: The x-values span from negative infinity to positive infinity. However, the function appears to be discontinuous at certain points, specifically:
- There is an open circle at \(x = -3\).
- There is another open circle at \(x = 4\).
- **Range**: The y-values extend from negative infinity upwards:
- The lowest point of the curve appears to reach potentially \(-\infty\).
- The function is discontinuous at the following y-values:
- There is an open circle at \(y = -4\).
- There is another open circle at \(y = 4\).
The graph includes a curve with two distinct portions:
- The left portion starts from negative infinity, increases and reaches as high as \(y=4\) where an open circle is present before decreasing.
- The right portion starts at \(x=4\) increases up to a peak just below \(y=5\) and continues further right as it descends toward infinity.
### Interpretation for Domain and Range (using interval notation):
- **Domain**: The domain of function \(h\) can be described as \( (-\infty, -3) \cup (-3, 4) \cup (4, \infty) \).
- **Range**: The range of function \(h\) is \( (-\infty, 4) \). The function does not reach the value \(y = 4\) at \(x = 4\).
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps

Knowledge Booster
Similar questions
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

