
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
The Dirac delta-function obeys: see image 1
a). Prove that: see image 1
b). see image 2
c). Now briefly describe how this result can be generalised to g(x) with n simple roots at {x1,x2,...,xn}
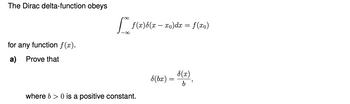
Transcribed Image Text:The Dirac delta-function obeys
for any function f(x).
a) Prove that
[ f(x)d(x − xv)dx = f(xv)
·∞
where b> 0 is a positive constant.
8(bx) =
h(r)
9

Transcribed Image Text:b)
=
It can be shown that for arbitrary b, 8(bx) = $(), and more generally, 8(b(x − x)) =
You can assume these results for this part of the question:
8(x-xo)
|b|
8(x-xo)
= |g'(xo)|*
i) Consider a function g(x) with one simple root at x = xo. Show that 8(g(x)) =
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 4 steps with 3 images

Knowledge Booster
Similar questions
- 7.0 refer to imagearrow_forwarda) The roots of a degree 4 polynomial f(x) are 0, –1, 1, 1. Suppose f(2) = -1. Find a formula for f(x). b) On what intervals is the above function positive? c) On what intervals is the above function negative?arrow_forwardb) Find the order of Z=0 for the 25 1) 1+2-e² following functions: 3) (e ²²-1-2²) Sin³z 2) 6 sin(z ³) + z⁹-6z³arrow_forward
- (b) Generate the graph of each of the following functions using the transfor- mation rules of graphs. i. f(x) = - cos(2x) in the interval [-27, 27] Rectangular Snip 1 g(r) = , sin (x -) in the interval [0, 27] ii. %3Darrow_forward(3) Compute an approximation of f(x) = tanx by computing the coefficients Co, C₁, C2, C3 (a = 0). Then graph y = tan x and the obtained cubic polynomial in the same coordinate system. As you zoom on the origin (0, 0) do these two graphs get closer?arrow_forwardIf f is a quadratic function such that f(0) = 9 and f(x) Fx + 1)3 is a rational.functian, find the value of f '(0). f '(0): Enter an exact number. Need Freip? Read Itarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

