Operations Research : Applications and Algorithms
Operations Research : Applications and Algorithms
4th Edition
ISBN: 9780534380588
Author: Wayne L. Winston
Publisher: Brooks Cole
Bartleby Related Questions Icon

Related questions

Q: Let S be a set of n lines in the plane such that no two are parallel and no three meet in the same…
A: Let S be a set of n lines in a plane such that notwo are parallel and no three meet in the same…
Q: 3) Show that the set of three-dimensional coordinates {(r,y, z)|x, y, z E Z} has size equal to N.
A: N stands for Natural numbers in number system.
Q: Draw a Bipartite Graph with 10 vertices that has an Eulerian Path and a Hamiltonian Cycle. The…
A: The solution to the given question is:
Q: Determine whether the graphs G and H are isomorphic. UĄ (b) VĄ U3 U5 V3 U2 V2 H G
A: Two graphs are isomorphic if they have: Equal number of vertices Number of vertices in graph G =…
Q: The graph Q5 has _vertices and --_edges. ---
A: Qn has 2n vertices, 2n-1n edges, and is a regular graph with n edges touching each vertex. Q5  25=32…
Q: Question 3: A graph G has order 24 and size 72. The degree of each vertex is 3, 6 or 9. There are 6…
A: When dealing with a graph, the order signifies the total number of vertices, while the size reflects…
Q: Q23. The following Adjacency Matrix represents 1 2 3 4 5 6 1030000 2000000 30 700 50 40 10000 5000…
A: The question has been solved in step2
Q: A rectangle has a perimeter of 20. If the area of the rectangle is to be maximized, the length of…
A: Answer
Q: Please use the Floyd-Warshall Algorithm to find the shortest paths for every two vertices. You need…
A: To apply the Floyd-Warshall algorithm to find the shortest path between all pairs of…
Q: Design an O(E) time algorithm for recognizing a palm polygon P where E is the number of visible…
A: an O(E) time algorithm for recognizing a palm polygon P where E is the number of visible pairs of…
Q: The time efficiency of warshall's algorithm for computing the transitive closure is (1) O Ⓒ(n³) O(n)…
A: The Floyd Warshall Algorithm is for solving all the pairs shortest path problems. The problems are…
bartleby

Concept explainers

Any Pair Segment
A line segment is the part of a line that is represented by a connection of two end points. It encompasses both ends of the line, as well as all points in between. The length of a line cannot be measured, but the length of a segment can be measured. If a…
Question

The Catalan number Cn gives the number possible non-intersecting diagonals in a a convex polygon with 2n vertices. The formula is

The Catalan number Cn gives the number possible non-intersecting polygon diagonals in a a convex
expand button
Transcribed Image Text:The Catalan number Cn gives the number possible non-intersecting polygon diagonals in a a convex
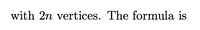
with 2n vertices. The formula is
expand button
Transcribed Image Text:with 2n vertices. The formula is
Expert Solution
Check Mark
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
bartleby
This is a popular solution
See solutionCheck out a sample Q&A here
Step 1
VIEW
C1, C2, C3, C4, C5 this is additional part
VIEW
Step 3
VIEW
bartleby

Trending nowThis is a popular solution!

bartleby

Step by stepSolved in 3 steps with 3 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Computer Science
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Operations Research : Applications and Algorithms
Computer Science
ISBN:9780534380588
Author:Wayne L. Winston
Publisher:Brooks Cole
SEE MORE TEXTBOOKS