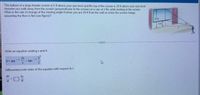
The bottom of a large theater screen is 6 ft above your eye level and the top of the screen is 20 t above your eye level Assume you walk away from the screen (perpendicular to the screen) at a rate of 2 fis while looking at the screen What is the rate of change of the viewing angle 0 when you are 20 t from the wall on which the screen hangs. assuming the floor is flat (see figure)? 20 m Write an equation relating x and 0 20 tan 0= tan Differentiate both sides of the equation with respect to t do dt

Q5: As a hot-air balloon began to rise, the ground crew drove 1.2 miles to an observation station. The initial observation from the station estimated the angle between the ground and the line of sight to the balloon to be 30°. Calculate distance "h" and "x" given in the diagram below. h 1.2 mi 30%

Please written by computer source A ladder ?=13 m long is leaning against a wall. If the lower end of the ladder slides away from the wall at the rate of ?=0.5 m/s, at what rate is the inclination ? of the ladder with respect to the ground changing when the lower end is 4 m from the wall?

Click the play button and note the values of the angular speed w, and the linear speed v. (i) How does decreasing the radius affect the linear speed? (ii) How does increasing the radius affect the angular speed? Use the interactive figure to find your answer. Use the left and right arrow keys to move along a slider as needed. Click here to launch the interactive figure. (1) Choose the correct answer below. O A. When the radius decreases the linear speed increases. B. When the radius decreases the linear speed stays the same. C. When the radius decreases the linear speed decreases. (ii) Choose the correct answer below. O A. When the radius increases the angular speed increases. O B. When the radius increases the angular speed stays the same. O C. When the radius increases the angular speed decreases.