Question
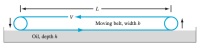
Transcribed Image Text:### Diagram Explanation: Moving Belt in Oil
This diagram illustrates a moving belt system interacting with oil.
#### Key Components:
1. **Moving Belt (blue line):**
- The belt is depicted with blue lines and arrows.
- The belt has a certain width, denoted as \( b \).
- The belt moves horizontally with a velocity \( V \).
2. **Oil Bath (grey region):**
- The belt partially submerges in oil to a depth \( h \).
- The oil is represented by the grey region in the diagram.
3. **Supporting Rollers:**
- Two circular rollers are shown on either side of the diagram, guiding the belt's movement.
- The arrows at the sides where the belt goes in and out of the oil bath indicate the direction of motion.
4. **Dimensions:**
- The length of the belt interacting with the oil is denoted by \( L \).
- \( h \) represents the depth of the oil into which the belt is submerged.
### Detailed Breakdown:
- **Length of Interaction (L):** The belt makes contact with the oil over a horizontal length denoted by \( L \).
- **Belt Width (b):** The width of the moving belt is marked as \( b \).
- **Belt Velocity (V):** The belt moves at a velocity \( V \)—shown by the leftward pointing arrows on the blue belt.
- **Oil Depth (h):** The oil depth, where the belt submerges, is noted as \( h \).
### Application:
This diagram can be used to explain fluid dynamics and mechanical interactions between moving surfaces and fluids in various engineering contexts, such as lubrication, cooling systems, or even certain types of manufacturing processes.
Feel free to use this breakdown for educational purposes to provide a clear understanding of the system illustrated by this diagram.
![### Belt Skimming over Tank of Oil: Power Calculation
**Problem Statement:**
The belt in Fig. P1.52 moves at a steady velocity \( V \) and skims the top of a tank of oil with viscosity \( \mu \), as illustrated. Assuming a linear velocity profile in the oil, develop a simple formula for the required belt-drive power \( P \) as a function of \( (h, L, V, b, \mu) \).
**Question:**
What belt-drive power \( P \), in watts, is required if the belt moves at 2.5 m/s over SAE 30W oil at 20°C, with \( L = 2 \) m, \( b = 60 \) cm, and \( h = 3 \) cm?
### Solution Outline:
1. **Understanding Variables:**
- **\( V \):** Velocity of the belt (m/s)
- **\( \mu \):** Viscosity of the oil (Pa·s or N·s/m²)
- **\( L \):** Length of the belt (m)
- **\( b \):** Width of the belt (m)
- **\( h \):** Thickness of the oil layer (m)
2. **Assumptions:**
- Linear velocity profile in the oil
- The belt skims the top, implying interaction mainly at the surface layer.
3. **Formula Development:**
The drag force \( F \) exerted by the oil on the belt can be found using Newton's law of viscosity:
\[
F = \mu \frac{V}{h} A
\]
where \( A = L \times b \) (area of the belt interacting with the oil).
Therefore,
\[
F = \mu \frac{V}{h} (L \times b)
\]
4. **Power Calculation:**
Power \( P \) required to overcome this drag force at steady velocity \( V \) is given by:
\[
P = F \times V = \left( \mu \frac{V}{h} (L \times b) \right) \times V = \mu \frac{V^2}{h} L b
\]
5. **Substitution:**
Substituting the given values](https://content.bartleby.com/qna-images/question/508ae4f5-8e9f-43cb-9ab2-37d719369fa8/e05de107-e38f-41ae-a6a8-01552dd135e3/d2d0ii_thumbnail.png)
Transcribed Image Text:### Belt Skimming over Tank of Oil: Power Calculation
**Problem Statement:**
The belt in Fig. P1.52 moves at a steady velocity \( V \) and skims the top of a tank of oil with viscosity \( \mu \), as illustrated. Assuming a linear velocity profile in the oil, develop a simple formula for the required belt-drive power \( P \) as a function of \( (h, L, V, b, \mu) \).
**Question:**
What belt-drive power \( P \), in watts, is required if the belt moves at 2.5 m/s over SAE 30W oil at 20°C, with \( L = 2 \) m, \( b = 60 \) cm, and \( h = 3 \) cm?
### Solution Outline:
1. **Understanding Variables:**
- **\( V \):** Velocity of the belt (m/s)
- **\( \mu \):** Viscosity of the oil (Pa·s or N·s/m²)
- **\( L \):** Length of the belt (m)
- **\( b \):** Width of the belt (m)
- **\( h \):** Thickness of the oil layer (m)
2. **Assumptions:**
- Linear velocity profile in the oil
- The belt skims the top, implying interaction mainly at the surface layer.
3. **Formula Development:**
The drag force \( F \) exerted by the oil on the belt can be found using Newton's law of viscosity:
\[
F = \mu \frac{V}{h} A
\]
where \( A = L \times b \) (area of the belt interacting with the oil).
Therefore,
\[
F = \mu \frac{V}{h} (L \times b)
\]
4. **Power Calculation:**
Power \( P \) required to overcome this drag force at steady velocity \( V \) is given by:
\[
P = F \times V = \left( \mu \frac{V}{h} (L \times b) \right) \times V = \mu \frac{V^2}{h} L b
\]
5. **Substitution:**
Substituting the given values
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Buoyant force is a vector. The direction of the buoyant force is ? A. upward only B. Depends on the weight of the object C. sideways (right and left) D. Down wardarrow_forwardBlock Suspended in Alcohol - Numerical Problem A glass bowl containing 350 mL of alcohol with a density of 0.868 g/mL rests on a scale that reads 4.02 N (including the weight of the bowl). Then, a 57.0 cm³ block of material with a mass 370 g of is held in the alcohol by a thread, in such a way that the block does not touch any part of the bowl and no alcohol overflows. (Figure 1) Figure 1 of 1 Part A What is the tension in the thread? Enter the tension in Newtons to three significant digits. FT = Submit Part B IT ΑΣΦ Request Answer What is the new reading on the scale? www ? Narrow_forwardWhich of the following can be explained by the Bernoulli equation? A. curveball B. "Bending" a soccer ball C. The lift on an airplane wing D. All of the abovearrow_forward
arrow_back_ios
arrow_forward_ios